文档维护:Arvin
网页部署:Arvin
▶
写在前面:
全局规划算法与局部规划算法,全局规划属于静态规划,局部规划属于动态规划。
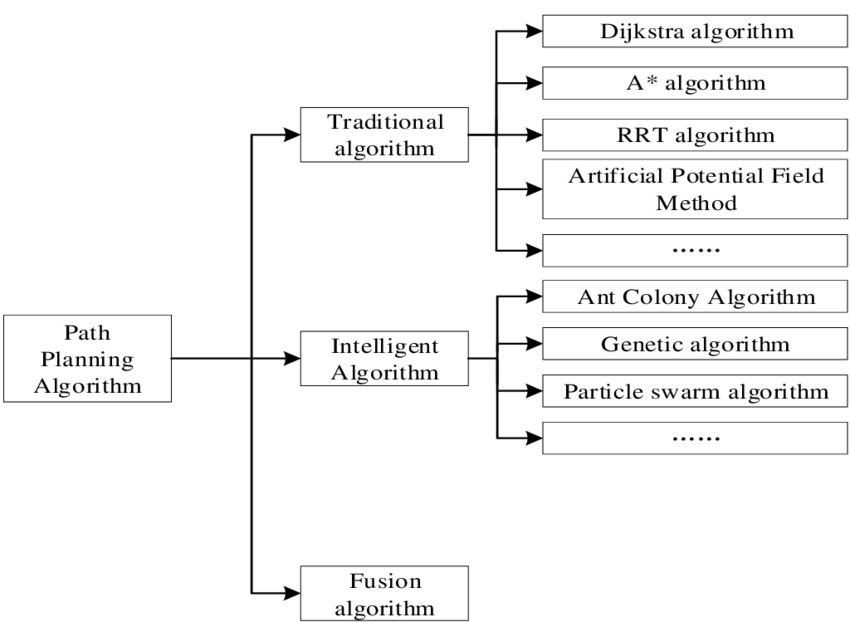
全局规划算法
A*算法
A*算法是一种很常用的路径查找和图形遍历算法。
首先我们需要知道地图信息(栅格地图)、起点位置、终点位置。
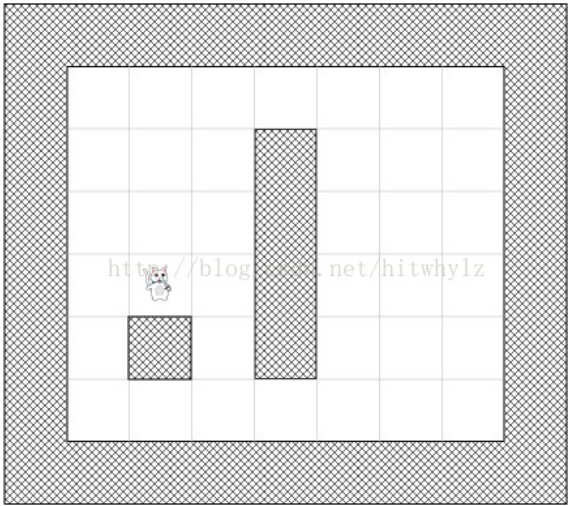
然后开始搜索计算每个点的优先级。其核心是下面这个公式:
f(n)=g(n)+h(n)
公式是为了求得节点优先级,其中:
- f(n)是节点
n的综合优先级。当选择下一个要遍历的节点时,总会选择综合优先级最高的(值最小)的节点。
- g(n)是节点n距离起点的代价,即节点
n与起点的距离。
- h(n)是节点n距离终点的预计代价,也就是A*算法的启发函数,一般采取节点
n到终点的曼哈顿距离。
g(n)是从开始点到当前点的移动量:
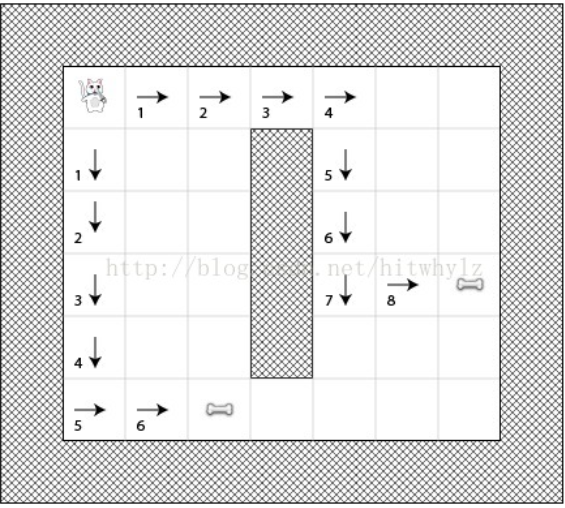
h(n)采用曼哈顿距离计算:
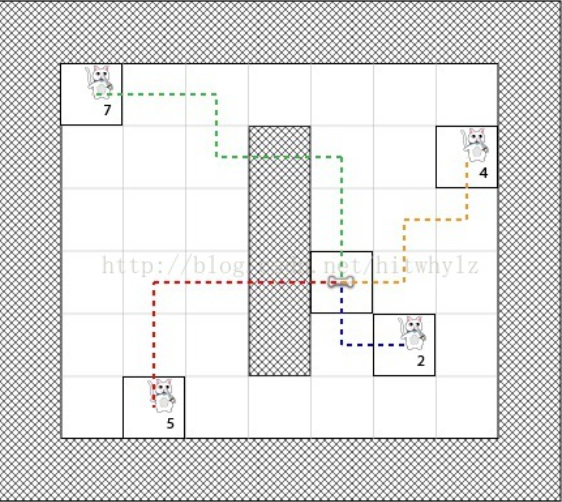
然后根据算法进行搜索:
- 初始化open_set和close_set;
- 将起点加入open_set中,并设置优先级为0(优先级最高);
- 如果open_set不为空,则从open_set中选取优先级最高的节点n:
- 如果节点n为终点,则:
- 从终点开始逐步追踪parent节点,一直达到起点;
- 返回找到的结果路径,算法结束;
- 如果节点n不是终点,则:
- 将节点n从open_set中删除,并加入close_set中;
- 遍历节点n所有的邻近节点:
- 如果邻近节点m在close_set中,则:
- 如果邻近节点m也不在open_set中,则:
- 设置节点m的parent为节点n
- 计算节点m的优先级
- 将节点m加入open_set中
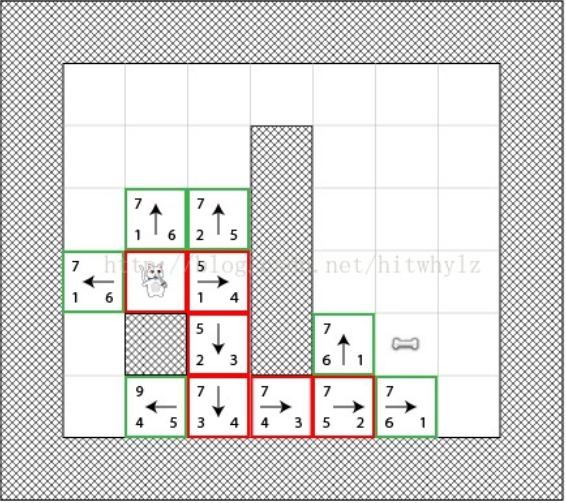
简单的代码实现:
局部规划算法
DWA(Dynamic Window Approach)
DWA算法(dynamic window approach),其原理主要是在速度空间(v,w)中采样多组速度,并模拟出这些速度在一定时间内的运动轨迹,并通过评价函数对这些轨迹进行评价,选取最优轨迹对应的(v,w)驱动机器人运动。
机器人运动学
根据下式,机器人在很短时刻内,我们可以将相邻两点之间的运动轨迹看成直线,我们就可以根据速度来推断机器人的运动轨迹。
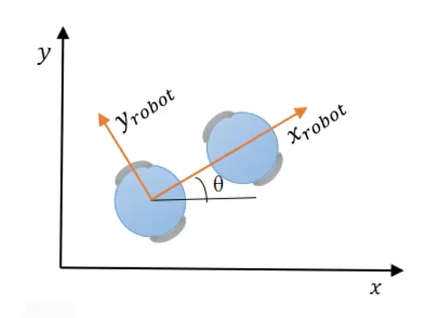
差速机器人:机器人只能向前运动x轴线速度v或者旋转z轴角速度w。
x(t+Δt)y(t+Δt)v(t+Δt)θ(t+Δt)ω(t+Δt)=x(t)+v(t)∗cos(θ(t))∗Δty(t)+v(t)∗sin(θ(t))∗Δtv(t)+a(t)∗Δtθ(t)+ω(t)∗Δtω(t)+α(t)∗Δt
全向机器人:在机器人坐标系中,不仅有x方向的速度vx,还有y方向的速度vy,另外还可以旋转w。
x(t+Δt)y(t+Δt)vx(t+Δt)vy(t+Δt)θ(t+Δt)ω(t+Δt)=x(t)+vx(t)∗cos(θ(t))∗Δt−vy(t)∗sin(θ(t))∗Δty(t)+vx(t)∗sin(θ(t))∗Δt+vy(t)∗cos(θ(t))∗Δtvx(t)+ax(t)∗Δtvy(t)+ay(t)∗Δtθ(t)+ω(t)∗Δtω(t)+α(t)∗Δt
约束
有了运动学模型,就可以根据速度推算出轨迹,但是速度是有约束的,我们可以采样到的速度是有限制的。
-
移动机器人受自身最大速度最小速度的限制
Vs为机器人能够到达的所有矢量速度的集合;机器人受到最大最小线速度和角速度影响。
Vs={(v,ω)∣v∈[vmin ,vmax ]∧ω∈[ωmin ,ωmax ]}
-
受电机性能的影响
由于加速度有一个范围限制,所以最大加速度或最大减速度一定时间内能达到的速度 ,才会被保留,即速度会有一个分辨率,表达式如下:
Vd={(v,ω)∣v∈[vc−v˙bΔt,vc+v˙aΔt]∧ω∈[ωc−ω˙bΔt,ωc+ω˙aΔt]}
-
受障碍物的影响
要有一个刹车距离,为了能在碰到障碍物前停下来,在最大减速度的条件下,速度满足以下条件:
Va={(v,ω)∣v≤2dist(v,ω)v˙b∧ω≤2dist(v,ω)ω˙b}
其中dist(v,w)为(v,w)对应的轨迹上里障碍物最近的距离。
在上述三条约束条件的限制下,速度空间(v,w)会有一定的范围,另外会随着电机的线加速度、角加速度进行变换,速度空间会动态变化,我们将其称为动态窗口。在满足约束条件的情况下,进行采样(v,w),可以得到相应的轨迹:
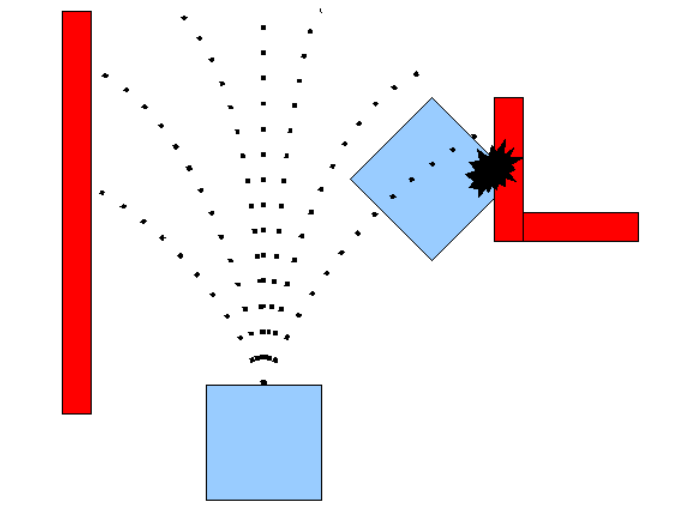
评价函数
在得到许多条轨迹后,我们就根据评价函数挑选最优路径,一般来说,评价函数如下:
G(v,ω)=σ(α∗ heading (v,ω)+β∗dist(v,ω)+γ∗vel(v,ω))
其中,heading(v,w)为方位角评价函数:评价机器人在当前的设定的速度下,轨迹末端朝向与目标点之间的角度差距;$dist(v,w) $ 主要的意义为机器人处于预测轨迹末端点位置时与地图上最近障碍物的距离,对于靠近障碍物的采样点进行惩罚,确保机器人的避障能力,降低机器人与障碍物发生碰撞的概率;velocity(v,w)为当前机器人的线速度,为了促进机器人快速到达目标; α 、 β 、 γ 、 σ 为权重。当然,可以对评价函数进行优化,添加更多的评价函数指标。
参考链接:
A星算法
DWA算法
ROS官方代码实现








