Arvin

文档维护：Arvin 网页部署：Arvin ▶ 写在前面：HEXO搭建个人博客 HEXO个人博客搭建 参考链接1参考链接2 环境准备安装Node.js参考链接 Node.js 是一个开源的、跨平台的 JavaScript 运行时环境，它允许开发者在服务器端运行 JavaScript 代码。Node.js 最初由 Ryan Dahl 于 2009 年创建，目的是为了构建高性能的网络应用。下载官网 下载后开始安装 更改安装位置不要安装在C盘，其余默认即可。安装后打开终端，输入以下命令查看是否安装成功 在刚才的安装位置中新建两个文件夹node_global和node_cache，然后在终端中输入命令更改下载缓存位置 按照下列步骤配置文件 更改环境变量 然后把下面的“C:\User\AppData\Roaming\npm”修改为“D:\Program\nodejs\node_global”，即可 安装git点击下载链接下载安装程序按照步骤安装即可（更改安装路径，其余默认即可）。 安装hexo 安装HEXO 1npm install -g hexo-cli ...

文档维护：Arvin 网页部署：Arvin ▶ 写在前面：Ubuntu20.04和Windows系统安装教程 vectory系统盘制作 官方链接 Ubuntu安装教程软件安装搜狗拼音 参考链接： Ubuntu20.04安装搜狗输入法 安装fcitx 12sudo apt install fcitx-binsudo apt-get install fcitx-table 下载搜狗安装包 搜狗输入法官网 安装依赖 12sudo apt install libqt5qml5 libqt5quick5 libqt5quickwidgets5 qml-module-qtquick2sudo apt install libgsettings-qt1 安装搜狗 12cd ~/Downloads/sudo dpkg -i sogoupinyin_4.2.1.2800_x86_64.deb # 依照自己的文件名字确定 切换fcitx 在系统设置Settings中选择region and languages，点击Manege installed language。 先把下面选...

文档维护：Arvin 网页部署：Arvin ▶ 写在前面：本文内容是作者在深蓝学院自动驾驶预测与决策规划学习时的笔记，作者按照自己的理解进行了记录，如果有错误的地方还请执政。如涉侵权，请联系删除。 时空联合规划传统的时空分离规划只考虑了路径规划和速度规划，分别对应横向控制和纵向控制。而时空联合规划算法则同时考虑空间和时间来规划轨迹，在路径基础上再求解速度从而形成轨迹，能够能直接在$x-y-t$（即平面和时间）三个维度的空间中直接求解最优轨迹。 时空分离规划： 时空联合规划： 基于搜索（Hybrid A*）的时空联合规划方法构建三维时空联合规划地图 构建二维栅格地图 二维x-y栅格地图只具有几何属性，无法直接搜索带有时间属性的可行驶轨迹。 （灰色圆形区域部分：在最大转向角下也会发生碰撞 或 不可能到达目的地 ； ​ 半径大小：最小转弯半径； ​ 方向：车速方向相切；） 沿时间轴扩展生成三维时空地图 如下图所示，多个地图层相互平行；相邻图层中的两个状态根据时间步长由有向边相连；蓝色有向边连接的点序列表示以$\Delta t$为时间步长离散化的时空轨迹；绿色部分：动...

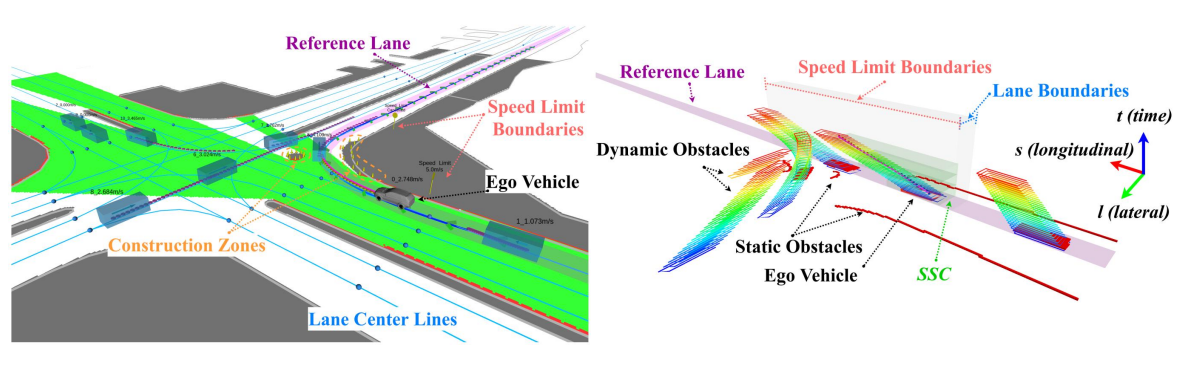
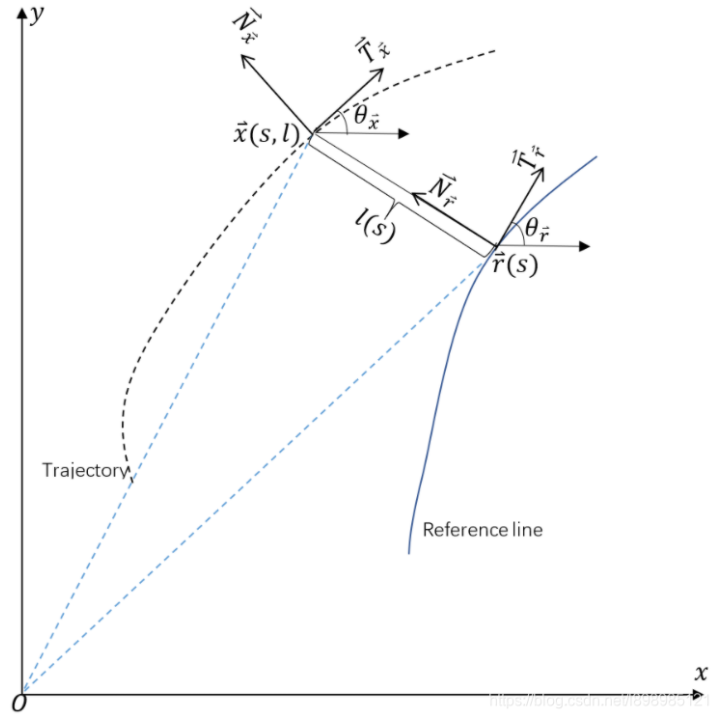
文档维护：Arvin 网页部署：Arvin ▶ 写在前面：本文内容是作者在深蓝学院自动驾驶预测与决策规划学习时的笔记，作者按照自己的理解进行了记录，如果有错误的地方还请执政。如涉侵权，请联系删除。 规划算法（笔记）路径与轨迹规划（笔记）基于搜索的路径规划Hybrid A*算法 节点的拓展基于车辆运动学模型 代价的计算基于栅格栏 代价计算 代价包括节点遍历代价和两个启发函数，即$F(n)=g(n)+h_1(n)+h_2(n)$，其中 $g(n)$主要考虑路径长度、运动学约束、方向变换成本; $h_1(n)$只考虑车辆的运动学约束而不考虑障碍物; $h_2(n)$只考虑障碍物信息而不考虑车辆的运动学约束; 基于采样的路径规划Frenet坐标系 Werling M , Ziegler J , Kammel S , et al. Optimal Trajectory Generation for Dynamic Street Scenarios in a Frenet Frame[C]// Robotics and Automation (ICRA), 2010 IEEE Inte...

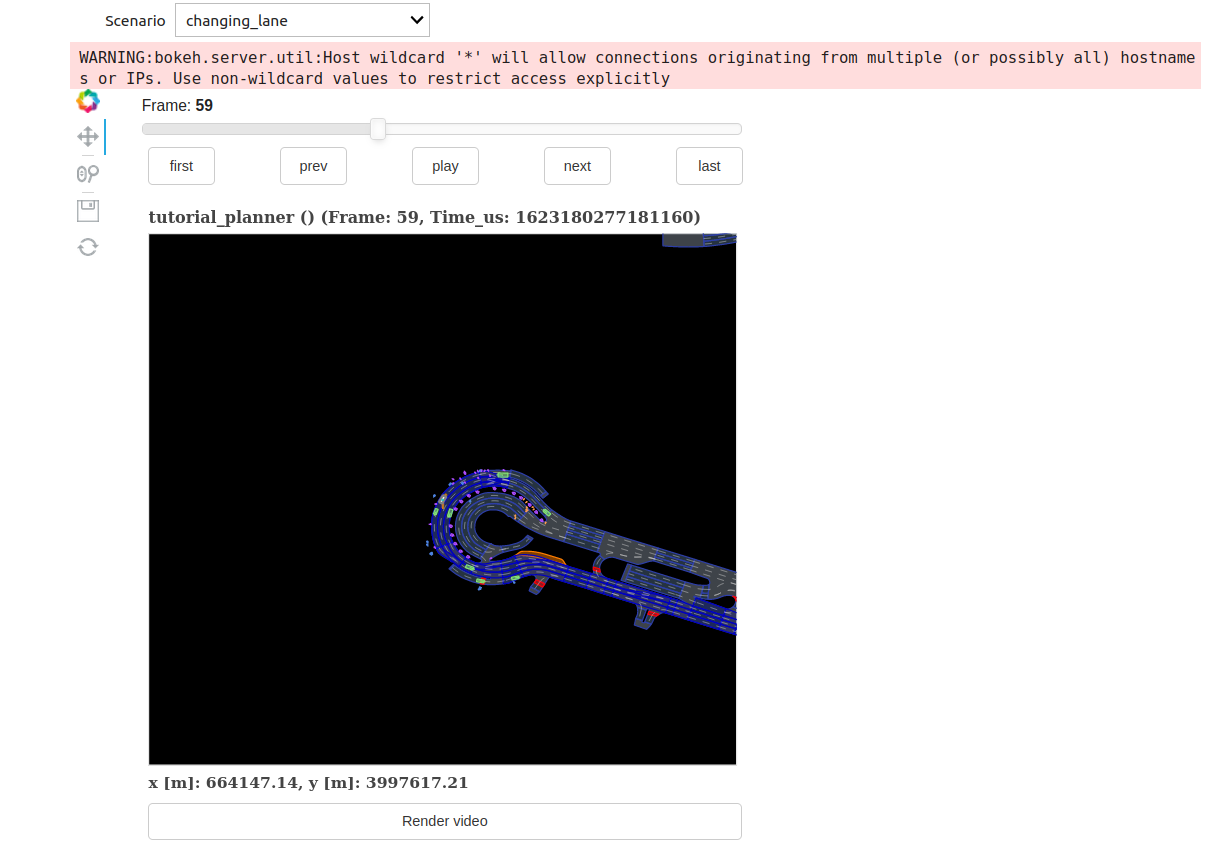
文档维护：Arvin 网页部署：Arvin ▶ 写在前面：本文内容是作者在深蓝学院自动驾驶预测与决策规划学习时的笔记，作者按照自己的理解进行了记录，如果有错误的地方还请执政。如涉侵权，请联系删除。 自动驾驶决策规划简介实验准备下载nuplan-devkit在终端中进入希望的安装目录，以主目录为例，运行代码拉取命令： 12cd ~git clone https://github.com/motional/nuplan-devkit.git 安装miniconda在终端中输入以下命令下载miniconda安装包： 12cd ~wget https://repo.anaconda.com/miniconda/Miniconda3-latest-Linux-x86_64.sh 运行安装包，安装过程中按照指示一直按enter和选择yes即可： 1bash Miniconda3-latest-Linux-x86_64.sh conda全局初始化将conda的环境路径添加到用户目录的.bashrc文件中，终端每次启动时执行.bashrc添加conda的环境路径，初始化后重新启动终端即可使用co...

文档维护：Arvin 网页部署：Arvin ▶ 写在前面：本文内容是作者在深蓝学院机器人中的数值优化学习时的笔记，作者按照自己的理解进行了记录，如果有错误的地方还请执政。如涉侵权，请联系删除。 附录(笔记)函数的光滑技巧Inf convolution卷积Inf convolution 卷积操作适应于凸函数，Inf convolution 卷积操作的目标是把不光滑的凸函数进行光滑近似，并使得光滑近似后的函数于原函数尽量吻合。    对于两个凸函数$f_1， f_2$，它们之间的Inf convolution 卷积操作记为$f_1\Box f_2$，即找一个$u_1$和$u_2$，满足$u_1+u_2=x$的条件下，使得$f_1(u_1)+f_2(u_2)$最大或最小，如下面的第一个表达式所示，由于满足$u_1+u_2=x$，因此可消去一个$u$进行简化，简化后的表达式如下面第二个式子所示： \begin{aligned}(f_1\Box f_2)(x)&=\inf_{(u_1,u_2)\in\mathbb{R}^d\times\mathbb{R}^d}\{f_1(u_1)+f...

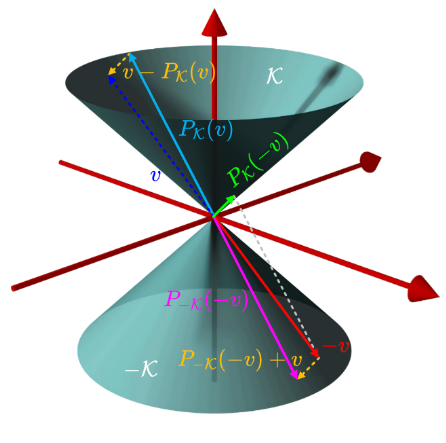
文档维护：Arvin 网页部署：Arvin ▶ 写在前面：本文内容是作者在深蓝学院机器人中的数值优化学习时的笔记，作者按照自己的理解进行了记录，如果有错误的地方还请执政。如涉侵权，请联系删除。 锥规划（笔记）锥和对称锥尖锥如果一组点$\kappa\subseteq\mathbb{R}^n$满足以下条件，则称为尖锥： \begin{aligned}&{\text{Conic:}\quad a\in\mathcal{K},\lambda\geq0\Rightarrow\lambda a\in\mathcal{K}}\\&{\text{Pointed:}\quad a\in\mathcal{K}\mathrm{~and~}-a\in\mathcal{K}\Rightarrow a=0}\end{aligned}第一个条件即向量$a$在集合$\mathcal{K}$中，$\lambda\geq0$，则$\lambda a$也必然在集合$\mathcal{K}$中；第二个条件是若向量$a$在集合$\mathcal{K}$中，则向量$-a$不在集合$\mathcal{K}$中，除非向量$a...

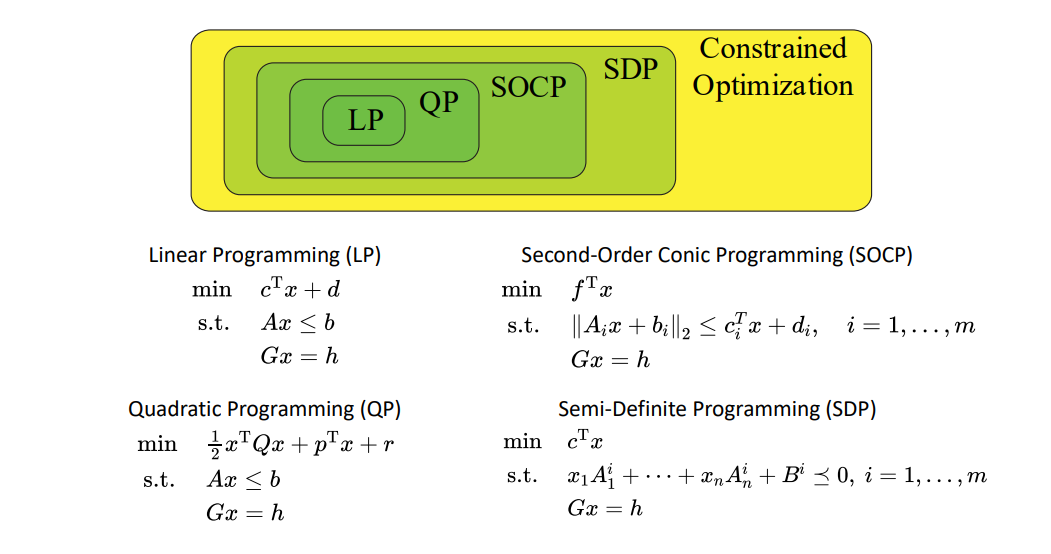
文档维护：Arvin 网页部署：Arvin ▶ 写在前面：本文内容是作者在深蓝学院机器人中的数值优化学习时的笔记，作者按照自己的理解进行了记录，如果有错误的地方还请执政。如涉侵权，请联系删除。 有约束优化（笔记）分类 低维线性规划（LP）目标函数： f(x_1,x_2\ldots x_d)=c_1x_1+c_2x_2+\cdots+c_dx_d约束： \begin{array}{l} a_{1,1} x_{1}+\cdots+a_{1, d} x_{d} \leqslant b_{1} \\ a_{2,1} x_{1}+\cdots+a_{2, d} x_{d} \leqslant b_{2} \\ a_{n, 1} x_{1}+\cdots+a_{n, d} x_{d} \leqslant b_{n} \\ \end{array} 每个约束表示$\mathbb{R}^d$中的一个半空间，半空间的交集形成可行域，可行域是$\mathbb{R}^d$中的凸多面体。 我们使$\vec{c}=(c_1,c_2,\ldots c_d)$（即目标函数梯度），沿此方向最前的那个点$v_{...

文档维护：Arvin 网页部署：Arvin ▶ 写在前面：本文内容是作者在深蓝学院机器人中的数值优化学习时的笔记，作者按照自己的理解进行了记录，如果有错误的地方还请执政。如涉侵权，请联系删除。 无约束优化拟牛顿法为什么要用拟牛顿法？一般情况下，当函数为曲线平滑的凸函数时，我们使用牛顿法。牛顿法如下： 通过二阶泰勒展开： f(\boldsymbol{x})\approx\hat{f}\left(\boldsymbol{x}\right)\triangleq f(\boldsymbol{x}_k)+\nabla f(\boldsymbol{x}_k)^T(\boldsymbol{x}-\boldsymbol{x}_k)+\frac12(\boldsymbol{x}-\boldsymbol{x}_k)^T\nabla^2f(\boldsymbol{x}_k)(\boldsymbol{x}-\boldsymbol{x}_k) \tag{1}最小化二次近似： \begin{aligned}&\nabla\hat{f}\left(\boldsymbol{x}\right)=\nab...

文档维护：Arvin 网页部署：Arvin ▶ 写在前面：本文内容是作者在深蓝学院机器人中的数值优化学习时的笔记，作者按照自己的理解进行了记录，如果有错误的地方还请执政。如涉侵权，请联系删除。 凸优化基础最优化问题概括最优化问题一般可以描述为： \begin{array}{rl}\min&f(x)\\\mathrm{s.t.}&g(x)\leq0\\&h(x)=0\end{array}凸集合与凸函数凸集对于$\mathbb{R}^{n}$中的两个点$x_{1}\ne x_{2}$，形如$y=\theta x_{1}+(1-\theta) x_{2}$的点形成了过点$x_{1}$和$x_{2}$的直线。当$0\le \theta \le1$，这样的点形成了连接点的$x_{1}$和$x_{2}$的线段。 定义：如果过集合C中任意两点的直线都在C内，则成C为放射集，即 \theta x_{1}, x_{2} \in C \Longrightarrow \theta x_{1}+(1-\theta) x_{2} \in C, \forall \theta \in \mathbb{R...