Adam
文档维护:Arvin
网页部署:Arvin
▶
Abstract
介绍了一种基于低阶矩自适应估计的随机目标函数一阶梯度优化算法Adam。该方法易于实现,计算效率高,内存需求少,对梯度的对角线重新缩放不变,非常适合数据和参数量大的问题。
该方法也适用于非平稳目标和具有非常嘈杂和/或稀疏梯度的问题。超参数有直观的解释,通常不需要调优。讨论了一些与相关算法的联系,这些算法是Adam的灵感来源。我们还分析了算法的理论收敛性,并给出了与在线凸优化框架下的最知名结果相当的收敛速度遗憾界。实证结果表明,Adam方法在实践中效果良好,优于其他随机优化方法。最后,我们讨论了基于无穷范数的Adam的变体AdaMax。
Introduction
Adam,一种只需要一节梯度且内存需求很小的高效随机优化方法。该方法通过估计梯度的第一阶矩和第二阶矩来计算不同参数的个体自适应学习率。算法伪代码:

参数:
- $t$:时间步数
- $\alpha$:学习率(步长)
- $\theta$:参数
- $f(\theta)$:目标函数(损失函数)
- $g_t$:梯度,即$g_t = \frac{\partial f}{\partial \theta}$
- $\beta_1$:一阶矩衰减系数,随时间减小,即$\beta_{1}^{t}$
- $\beta_2$:一阶矩衰减系数,随时间减小,即$\beta_{2}^{t}$
- $m_t$:一阶矩,即$g_t$均值
- $v_t$:二阶矩,即$g_t$方差
- $\hat{m_t}$:$m_t$的偏置矫正
- $\hat{v_t}$:$v_t$的偏置矫正
note:数学中,n阶矩就是一个量到某个参考点距离的n次方。物理学中,一阶矩描述的是物体匀速直线运动或者静止的量度,动量;二阶矩是保持匀速圆周运动或者静止的量度。
Algorithm
算法可以做如下改动,将循环中的最后三行替换为:
Adam中步长是有界限的。假设$\epsilon = 0$,时间步长$t$在参数空间中采取的有效步长为$\Delta_{t}=\alpha\cdot\widehat{m}_{t}/\sqrt{\widehat{v}_{t}}$,且有上届:
此外文章中还提到了置信域,超过这个信任域,当前梯度估计就不能提供足够的信息:
以及信噪比(signal-to-noise ratio, SNR):
对梯度的对角线重新缩放不变,用因子$c$重新缩放梯度$g$,则有:
Initialization Bias Correction
略
Convergence Analysis
略
Related Work
介绍了相关算法,如RMSProp、AdaGrad、SGD、AdaDelta等,主要介绍了和Adam联系紧密的RMSProp和AdaGrd:
RMSProp:与Adam密切相关的一种优化方法是RMSProp (Tieleman & Hinton, 2012)。有时会使用带有动量的版本(Graves, 2013)。带动量的RMSProp和Adam之间有一些重要的区别:带动量的RMSProp使用重新缩放的梯度上的动量来生成参数更新,而Adam更新是直接使用梯度的第一个和第二个矩的运行平均值来估计的。RMSProp也缺少偏差校正项;这在β2值接近1的情况下最重要(在稀疏梯度的情况下需要),因为在这种情况下,不纠正偏差会导致非常大的步长,并且经常出现分歧,正如我们在6.4节中经验证明的那样。
AdaGrad:AdaGrad (Duchi et al ., 2011)是一种适用于稀疏梯度的算法。其基本版本更新参数为:$\theta_{t+1}=\theta_{t}-\alpha\cdot g_{t}/\sqrt{\sum_{i=1}^tg_{t}^2}$。注意,如果我们从下面选择$\beta_2$无穷小地接近1,那么$\operatorname*{lim}_{\beta_{2}\rightarrow1}\widehat{v}_{t}=t^{-1}\cdot\sum_{i=1}^{t}g_{t}^{2}$。AdaGrad对应于一个$\beta_1 = 0$,无穷小$(1 - \beta_2)$的Adam版本,$\alpha$被$\alpha_t = \alpha\cdot t^{-1/2}$的退火版本取代,即:
请注意,当去掉偏差校正项时,Adam和Adagrad之间的这种直接对应关系不成立;如果没有偏差校正,比如在RMSProp中,$\beta_2$无穷小地接近1将导致无限大的偏差,以及无限大的参数更新。
Experiments
为了对提出的方法进行实证评估,我们研究了不同流行的机器学习模型,包括逻辑回归、多层全连接神经网络和深度卷积神经网络。通过使用大型模型和数据集,我们证明Adam可以有效地解决实际的深度学习问题。
- 逻辑回归
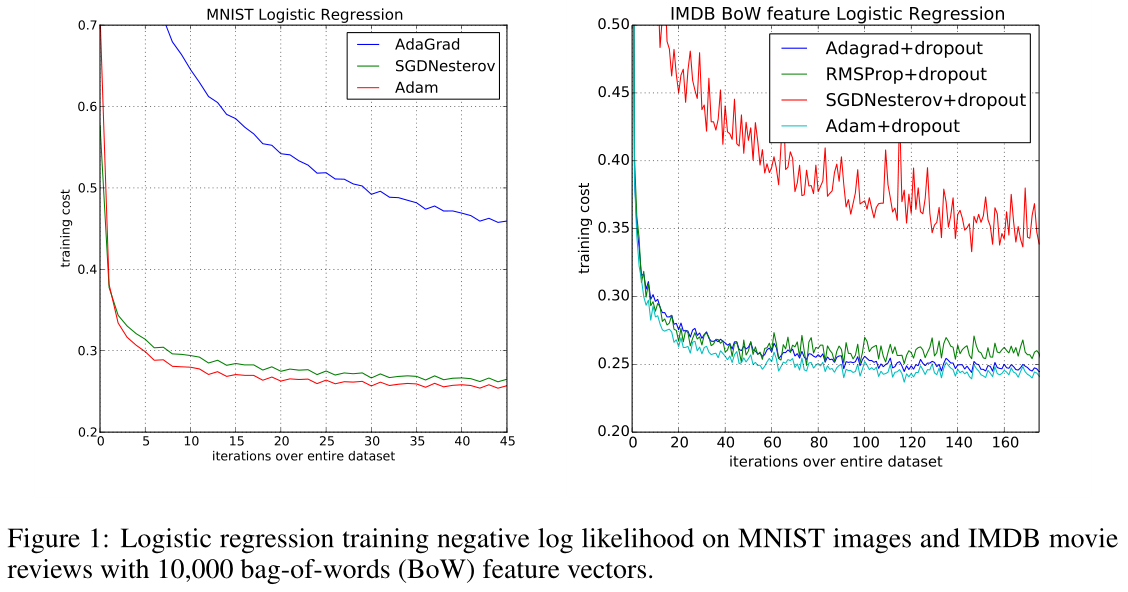
在图1中,Adagrad在有和没有dropout噪声的情况下,都大大优于SGD。Adam的收敛速度和Adagrad一样快。Adam的实验表现与我们在第2节和第4节中的理论发现是一致的。与Adagrad类似,Adam可以利用稀疏特征,获得比SGDNesterov更快的收敛速度。
- 深度神经网络
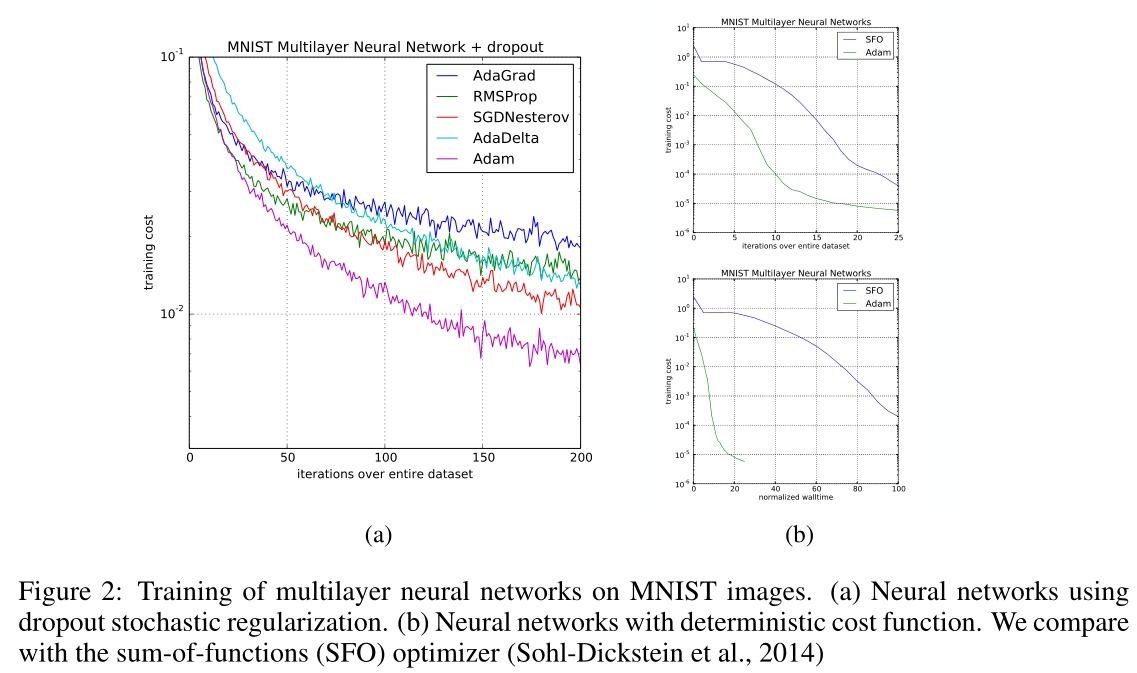
- 卷积神经网络
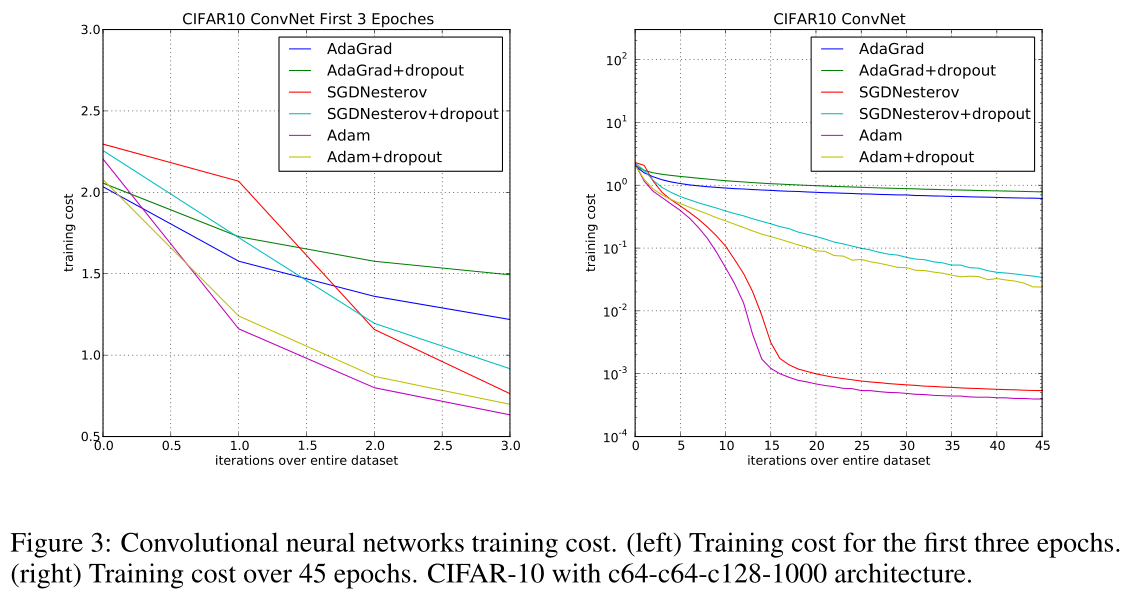
Extensions
ADAMAX

原文:Adam.pdf
引用:Kingma D P, Ba J. Adam: A method for stochastic optimization[J]. arXiv preprint arXiv:1412.6980, 2014.
参考资料: