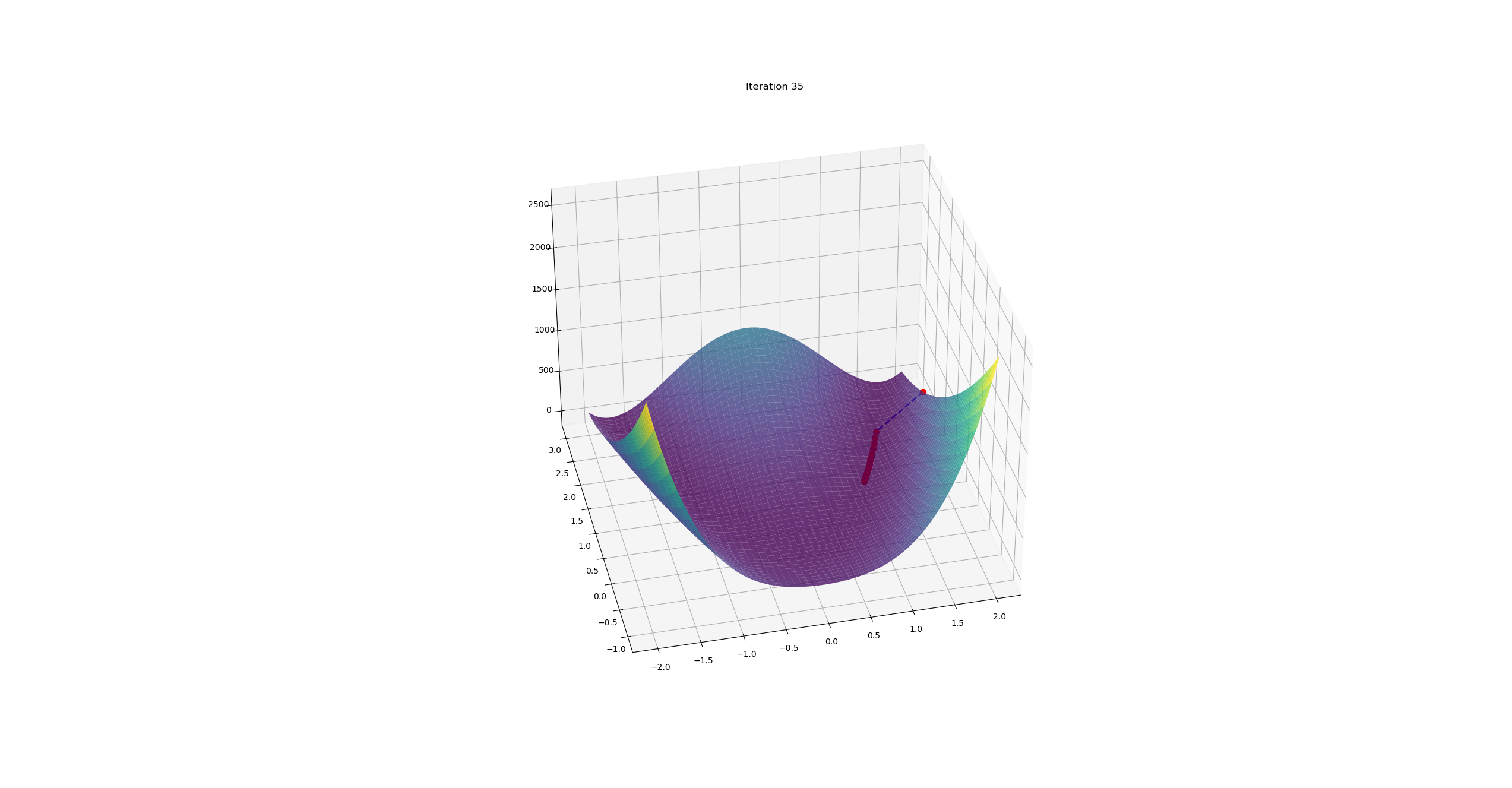
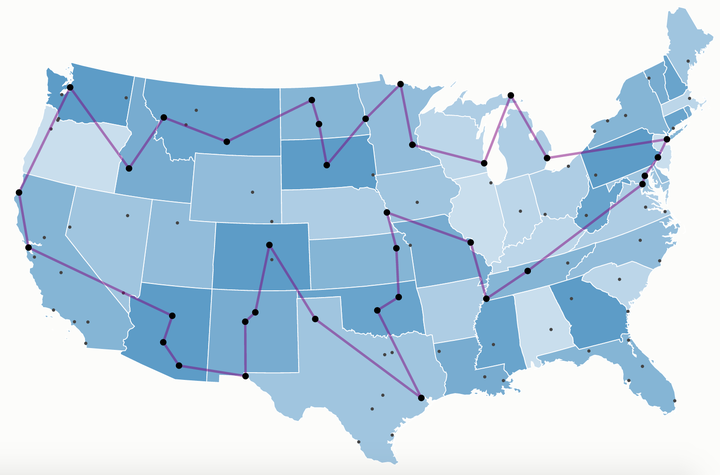
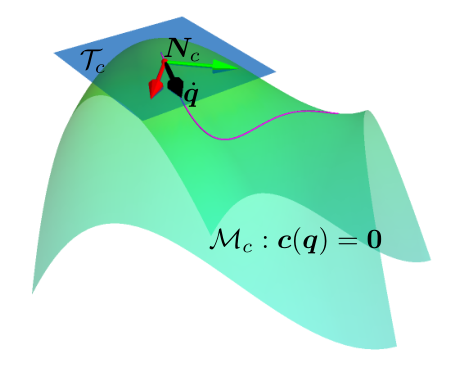
机器人中的数值优化(一)
文档维护:Arvin 网页部署:Arvin ▶ 写在前面:本文内容是作者在深蓝学院机器人中的数值优化学习时的笔记,作者按照自己的理解进行了记录,如果有错误的地方还请执政。如涉侵权,请联系删除。 凸优化基础最优化问题概括最优化问题一般可以描述为: \begin{array}{rl}\min&f(x)\\\mathrm{s.t.}&g(x)\leq0\\&h(x)=0\end{array}凸集合与凸函数凸集对于$\mathbb{R}^{n}$中的两个点$x_{1}\ne x_{2}$,形如$y=\theta x_{1}+(1-\theta) x_{2}$的点形成了过点$x_{1}$和$x_{2}$的直线。当$0\le \theta \le1$,这样的点形成了连接点的$x_{1}$和$x_{2}$的线段。 定义:如果过集合C中任意两点的直线都在C内,则成C为放射集,即 \theta x_{1}, x_{2} \in C \Longrightarrow \theta x_{1}+(1-\theta) x_{2} \in C, \forall \theta \in \mathbb{R...
AutoDL
文档维护:Arvin 网页部署:Arvin ▶ 写在前面:通过AutoDL平台租赁云服务器,配置环境,远程桌面。 vscode远程SSH链接参考链接:https://www.autodl.com/docs/ssh/ vscode安装插件SSH,添加SSH,输入SSH指令,点击connect,输入密码。 然后为remote添加常用的插件。 ros-melodic安装参考链接:http://www.autolabor.com.cn/book/ROSTutorials/chapter1/12-roskai-fa-gong-ju-an-zhuang/127-zi-65993a-qi-ta-ros-ban-ben-an-zhuang.html 安装源官方默认安装源: 1sudo sh -c 'echo "deb http://packages.ros.org/ros/ubuntu $(lsb_release -sc) main" > /etc/apt/sources.list.d/ros-latest.list' 或来自国内中科大的安装源 ...
TSP-RL
文档维护:Arvin 网页部署:Arvin ▶ TSP TSP问题(Traveling Salesman Problem),是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求所选的路径路程为所有路径中的最小值。 从图论的角度来看,TSP问题的输入是一个边带权的完全图,目标是找一个权值和最小的哈密顿回路。TSP问题可大致分为对称TSP问题和非对称TSP问题。所谓对称指的是在模型中,城市 u 到城市 v 的距离与城市 v 到城市 u 的距离是一样的,其在图中的体现就是对称TSP问题的输入一般是无向图,而非对称TSP问题的输入往往是有向图。本文主要讨论的是对称TSP问题。 假设给定一个 n 个点的带权完全图 G ,本文需要找到它权值和最小的哈密顿回路。或许会有人觉得这是求最短路,但是这并不是求最短路。最短路是求两点之间权值和最小的路径,而TSP求的是一个回路,并不能直接通过求解最短路进行求解。所有可能的路线共有$(n−1){!}$ 种 下面是两篇经典的使用神经网络和强化...
李群李代数(一)
文档维护:Arvin 网页部署:Arvin ▶ 写在前面:这篇的内容主要来自于《slam十四讲:从入门到实践》中的第三、四章,是为了引出李群李代数,文章大多记录了一些结论,如果对推导有兴趣可以去看书中详细的过程。 基础知识三维空间刚体运动旋转矩阵1.反对称矩阵 设$A=(a_{ij})_{n \times n}$,若其中元素满足$a_{ij}=a_{ji},\forall i,j\Leftrightarrow A^T=A$,则称$A$是对称矩阵;若其元素满足$a_{ij}=-a_{ji},\forall i,j\Leftrightarrow A^T=-A$,则称$A$为反对称矩阵。 若$A$是反对称矩阵,则$a_{ij}=-a_{ij}$,当$i=j$时,便有$a_{ij}=0$,即反对称矩阵对角线上的元全为零,而位于主对角线两侧对称的元素反号。 2.旋转矩阵 欧氏变换由旋转和平移组成。我们首先考虑旋转。设某个单位正交基$(e_1, e_2, e_3)$经过一次旋转变成了$(e^{\prime}_1, e^{\prime}_2, e^{\prime}_3)$。那么,对于同一个向...
RL in Constraint Manifold
文档维护:Arvin 网页部署:Arvin ▶ Abstract由于许多实际问题,包括安全、机械约束和磨损,机器人技术中的强化学习极具挑战性。 通常,这些问题在机器学习文献中没有被考虑。在现实世界中应用强化学习的一个关键问题是安全探索,这需要在整个学习过程中满足物理和安全约束。为了在这样一个安全关键的环境中进行探索,利用机器人模型和约束等已知信息有助于提供更强大的安全保证。利用这些知识,我们提出了一种新的方法,在满足学习过程中的约束的情况下,有效地学习仿真中的机器人任务。 Introduction深度强化学习虽然在一些问题上表现的很好,但是在现实世界中使用强化学习还是一项具有挑战性的任务,因为典型的强化学习算法,通过不断试错来最大化累计奖励,并没有考虑在探索过程中对约束的满足,而在实际世界中智能体在探索过程中要受到许多约束。 文章提出了一种新方法,在流形空间的切平面上执行动作(Acting on the Tangent Space of the Constraint Manifold, ATACOM)。该方法将约束强化学习问题转化成无约束强化学习问题。 ATACOM的优势可以概括...
Adam
文档维护:Arvin 网页部署:Arvin ▶ Abstract介绍了一种基于低阶矩自适应估计的随机目标函数一阶梯度优化算法Adam。该方法易于实现,计算效率高,内存需求少,对梯度的对角线重新缩放不变,非常适合数据和参数量大的问题。 该方法也适用于非平稳目标和具有非常嘈杂和/或稀疏梯度的问题。超参数有直观的解释,通常不需要调优。讨论了一些与相关算法的联系,这些算法是Adam的灵感来源。我们还分析了算法的理论收敛性,并给出了与在线凸优化框架下的最知名结果相当的收敛速度遗憾界。实证结果表明,Adam方法在实践中效果良好,优于其他随机优化方法。最后,我们讨论了基于无穷范数的Adam的变体AdaMax。 IntroductionAdam,一种只需要一节梯度且内存需求很小的高效随机优化方法。该方法通过估计梯度的第一阶矩和第二阶矩来计算不同参数的个体自适应学习率。算法伪代码: 参数: $t$:时间步数 $\alpha$:学习率(步长) $\theta$:参数 $f(\theta)$:目标函数(损失函数) $g_t$:梯度,即$g_t = \frac{\partial f}{\partia...