草稿
文档维护:Arvin
网页部署:Arvin
▶
写在前面:Ubuntu20.04和Windows系统安装教程
周记
决策过程(笔记)
决策过程的概念
马尔可夫决策过程
safe RL
将驾驶过程近似为马尔科夫过程,即下个状态只与当前状态有关系。
主要贡献:
-
**证明马尔科夫假设在策略梯度法中的不必要性;**使用策略梯度迭代的方法求解最优策略;使用baseline subtraction的方法,最小化对累积奖励估计的方差。
-
将问题分解为两个组成部分:一个是"Desires"策略,需要学习;而是带有硬约束的轨迹规划,不需要学习。“Desires”策略提高了驾驶的舒适性,轨迹规划的硬约束保证了驾驶的安全性;
-
引入有向无环图,即状态集。
MPDM: Multipolicy Decision-Making 多策略决策
- 将车辆行为建模成合理、安全的策略以减少不确定性;
- 通过前向模拟考虑周车对自身的影响;
- 评估不同策略下的模拟结果,选择最优的策略;

待解决问题:
- 周车的策略生命周期
- 后验更新
- 组合爆炸,关键场景
不确定性感知的决策过程
POMDP部分可观测马尔可夫决策过程
定义:
-
:状态集
-
:动作集
-
:一个集合,它指定给定前一个状态和动作的下一个状态的条件概率
-
:,奖励函数
是指在时刻状态下采取动作后获得的奖励。
-
:观测值的集合
-
:观测概率的集合,表示执行动作后,系统转移到状态后,观测值为的概率:
-
:,折扣因子
优化决策过程:
在POMDP中,智能体在每个时间步的动作决策取决于当前的置信状态。置信状态通过历史观测和动作进行更新。
智能体选择动作的策略是一个从置信状态到动作的映射,表示为。最优策略最大化从当前置信状态开始的期望折扣总奖励:
置信状态更新:
置信状态的更新取决于前一个置信状态,最后一个动作和最后观测值决定
表示环境处于状态的概率,已知,动作和观测,有:
举例:
老虎问题
求解
常规方法1:连续状态的“置信MDP”
常规方法2:
常规方法3:
端到端自动驾驶
Transfuser
提出了一种新颖的端到端驱动架构,主要包含两个方面。
- 用于融合多传感器模态(图像和雷达)的Transforms架构。
- 提出了一种自回归航路点预测网络。
Problem Setting
任务目标:城市环境中点对点导航任务,目标是在安全响应其他动态智能体并遵守交通规则的情况下完成给定路线。
**模仿学习(Imitation Learning):**模仿学习专家行为策略。本文完成的是输入到路径点的映射,然后路径点提供给单独的底层控制器输出动作。首先是专家数据集size大小为的,策略使用收集到的数据和损失函数以监督的方式进行训练。
**全局规划器:**遵循CARLA0.9.10的标准协议,假设高级目标位置是由GPS提供坐标,目标位置是稀疏的,可能相距数百米,而不是由策略预测的局部路径点。
Input and Output Parameterization
**输入:**雷达点云和RGB图像。
- 雷达:将雷达点云转换成固定分辨率的2D BEV网格上的2-bin直方图。本文考虑了自驾车前方32米内的点和两侧16米内的点,从而包含了一个32m × 32m的BEV网格。我们将网格划分为0.125m × 0.125m的块,得到256 × 256像素的分辨率。对于直方图,我们将高度维度离散成2 bins,分别代表地平面上/下和地平面上的点。我们还在与LiDAR点云相同的256 × 256 BEV空间中栅格化了2D目标位置,并将该通道连接到2 bins。这将产生一个大小为256 × 256像素的三通道伪图像。我们在BEV中表示目标位置,因为与透视图像域相比,这与路点预测的相关性更好。
- RGB图像:对于RGB输入,使用三个摄像头(面向前,60°左和60°右)。每个相机有一个水平视场120°。我们以960 × 480像素的分辨率提取图像,将其裁剪为320 × 160以消除边缘的径向畸变。这三个未失真的图像组成成一个单一的图像输入到编码器,其分辨率为704 × 160像素和132°FOV。
**输出:**以小车自身坐标系,预测小车在BEV空间中的未来轨迹。轨迹由一系列2D航路点组成,我们令,这是逆动力学模型所需的默认航路点数。
Multi-Model Fusion Transformer
本文的思想就是利用Transformers的自注意力机制将多模态传感器数据融合在一起。如下图所示:
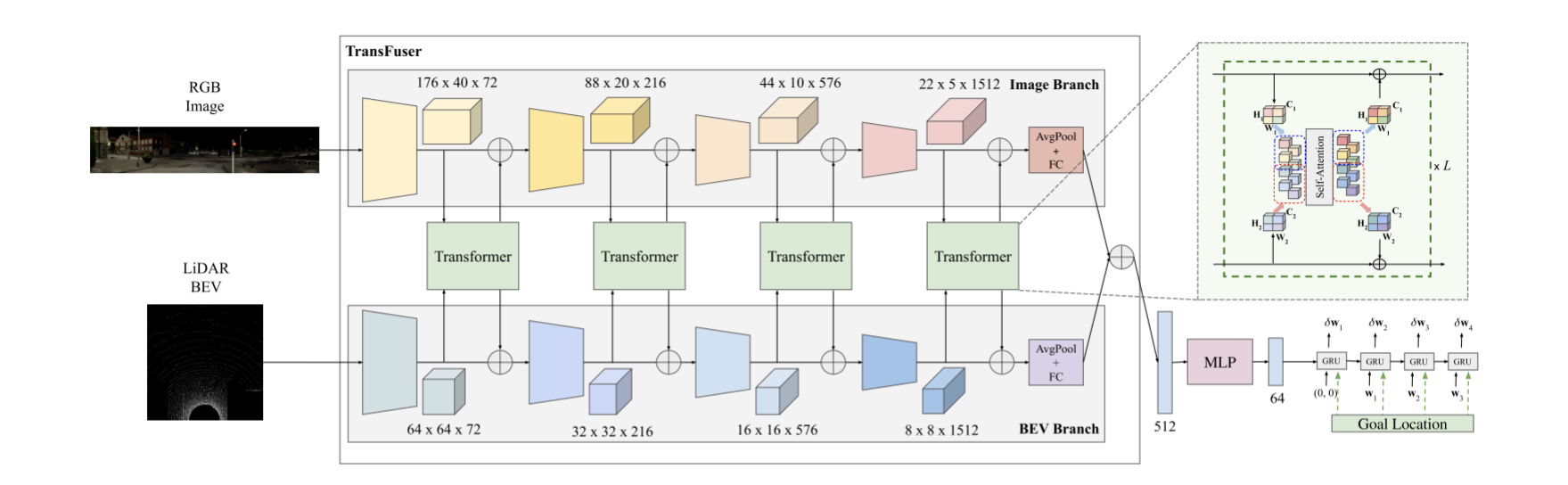
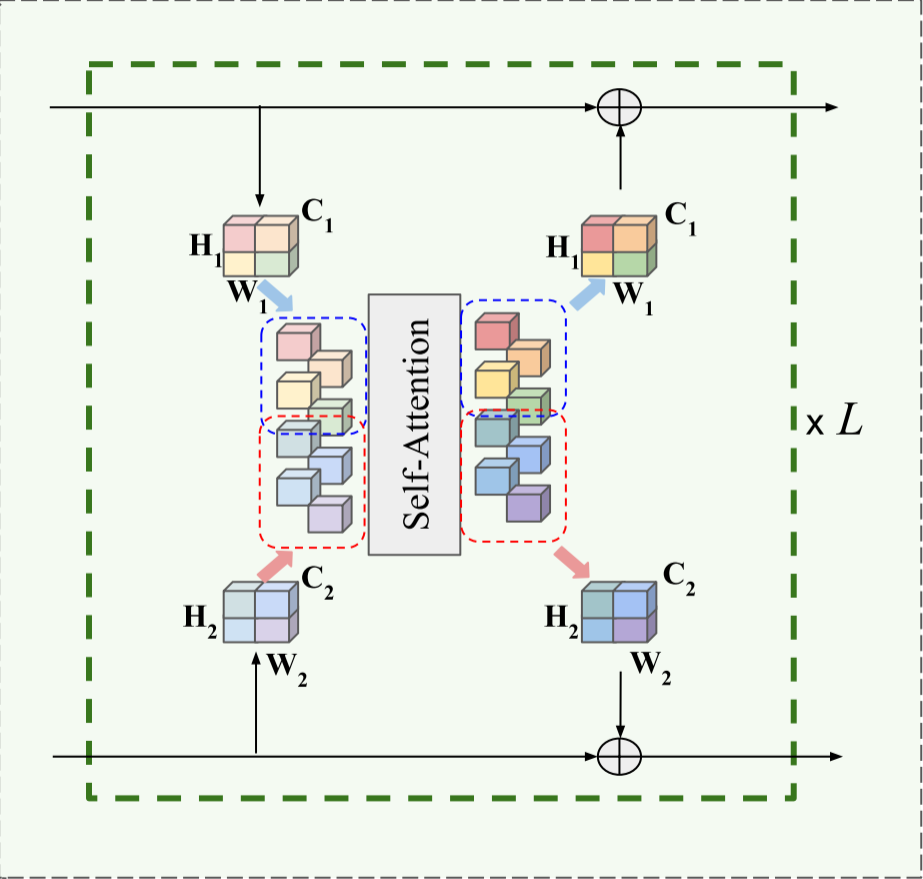
将输入序列表示为,表示序列的token数量,每个token用一个特征向量表示。Transformer使用线性投影计算一系列的:
其中都是权重矩阵。然后使用和之间的缩放点积来计算注意力权重,汇总每个query的值。
最后,transformer使用非线性变换计算输出特征,的shape和一样。
transformer在整个网络结构中多次应用注意力机制,从而产生个注意力层。
Waypoint Prediction Network
如图所示,为了提高计算效率,将512维特征向量通过MLP(包含256和128个单元的2个隐藏层)将其降维至64维,然后将其传递给使用gru实现的自回归路点网络。用64维特征向量初始化GRU的隐藏状态。GRU的更新门控制在隐藏状态下编码到输出和下一个时间步长的信息流。它还将当前位置和目标位置作为输入,这使得网络能够专注于隐藏状态下的相关上下文,以预测下一个路点。除了编码器之外,提供了目标位置的GPS坐标(注册到自我-车辆坐标框架)作为GRU的输入,因为它可以更直接地影响路点预测。之后使用一个单层GRU,然后是一个线性层,该线性层接受隐藏状态,并预测自我-车辆当前坐标系中T = 4个未来时间步长的微分路径点。因此,预测未来的路点由$\left<!–swig83–>=\mathrm{Ax}+\mathrm{Bu}\\mathrm{y}=\mathrm{Cx}+\mathrm{Du}\end{cases} \tag{1}
其中,$\mathrm{x}(t) \in \mathrm{R^n}, \mathrm{u}(t) \in \mathrm{R^m}$,初始条件是$\mathrm{x(0)}$。 在此,我们设计一个状态反馈控制器
\mathrm{u=-Kx} \tag{2}
\mathrm{\dot{x}=(A-BK)x=A_cx} \tag{3}
设定系统中的各个状态量都可知,式(1)所示的开环系统,传递函数的极点就是系统矩阵A的特征值。现在变换成了式(2)的闭环形式,通过配置反馈矩阵K KK,可以使得闭环系统达到所期望的系统状态。 ### LQR LQR的目标就是找到一组控制量$\mathrm{u_0}, \mathrm{u_1}, ...$使得同时有$\mathrm{x_0}, \mathrm{x_1}, ...$足够小(系统达到稳定状态),$\mathrm{u_0}, \mathrm{u_1}, ...$足够小(控制量进行小的变化),选取代价函数为
\mathrm J=\frac12 \int_0^\infty\mathrm x^\mathrm{T}\mathrm Q\mathrm x+\mathrm u^\mathrm{T}\mathrm R\mathrm u \mathrm d\mathrm t \tag{4}
其中,$Q, R$就是需要设计的半正定矩阵和正定矩阵。 1. 将$\mathrm{u}=-\mathrm{Kx}$代入代价函数,有
\mathrm J=\frac12 \int_0^\infty\mathrm x^\mathrm{T}(\mathrm Q+\mathrm K^\mathrm{T}\mathrm R\mathrm K)\mathrm x \mathrm d\mathrm t \tag{5}
2. 假设存在一个常量矩阵$P$使得,
\frac{\mathrm d}{\mathrm d\mathrm t}\left(\mathrm x^\mathrm{T}\mathrm P\mathrm x\right)=-\mathrm x^\mathrm{T}\left(\mathrm Q+\mathrm K^\mathrm{T}\mathrm R\mathrm K\right)\mathrm x \tag{6}
\mathrm J=-\frac{1}{2} \int_0^\infty\frac{\mathrm d}{\mathrm d\mathrm t}\mathrm x^\mathrm{T}(\mathrm P)\mathrm x =\frac{1}{2}\mathrm x^\mathrm{T}(0)\mathrm P\mathrm x(0) \tag{7}
式7的意思就是,t趋近于无穷时,系统状态向量$\mathrm{x(t)}$趋近于0,这样就直接结算除了积分方程。 4. 把式6左边微分展开
\mathrm x^\mathrm{T}\mathrm P\mathrm x+\mathrm x^\mathrm{T}\mathrm P\mathrm x+\mathrm x^\mathrm{T}\mathrm Q\mathrm x+\mathrm x^\mathrm{T}\mathrm K^\mathrm{T}\mathrm R\mathrm K\mathrm x=0
状态变量$\mathrm{x}$的微分用式3表示
\mathrm x^\mathrm{T}\mathrm A^\mathrm{T}\mathrm P\mathrm x+\mathrm x^\mathrm{T}\mathrm P\mathrm A_\mathrm{c}\mathrm x+\mathrm x^\mathrm{T}\mathrm Q\mathrm x+\mathrm x^\mathrm{T}\mathrm K^\mathrm{T}\mathrm R\mathrm K\mathrm x=0
\mathrm{x^T(A_c^{T}P~+PA_c+Q+K^T RK)x=0} \tag{8}
\mathrm{A_c^{T}P~+PA_c+Q+K^{T}RK=0} \tag{9}
把$A_c=A-BK$代入式9
\mathrm{(A-BK)^{T}P~+P(A-BK)+Q+K^{T}RK=0} \tag{10}
\mathrm A^\mathrm{T}\mathrm P+\mathrm P\mathrm A+\mathrm Q+\mathrm K^\mathrm{T}\mathrm R\mathrm K-\mathrm K^\mathrm{T}\mathrm B^\mathrm{T}\mathrm P-\mathrm P\mathrm B\mathrm K=0 \tag{11}
5. 式11还是一个关于$\mathrm{K}$的二次型,这样会导致计算量太复杂,我们令$\mathrm{K=R^{-1}B^{T}P}$,然后式11, 可以化为
\mathrm A^\mathrm{T}\mathrm P+\mathrm P\mathrm A+\mathrm Q+\mathrm K^\mathrm{T}\mathrm R(\mathrm R^{-1}\mathrm B^\mathrm{T}\mathrm P)-\mathrm K^\mathrm{T}\mathrm B^\mathrm{T}\mathrm P-\mathrm P\mathrm B(\mathrm R^{-1}\mathrm B^\mathrm{T}\mathrm P)=0
\mathrm A^\mathrm{T}\mathrm P+\mathrm P\mathrm A+\mathrm Q-\mathrm P\mathrm B\mathrm R^{-1}\mathrm B^\mathrm{T}\mathrm P=0 \tag{12}
式12中,$A, B, Q, R$都是已知量,那么通过式12可以求解出$P$,式12就是著名的Raccati方程。 ### 差速机器人 前面我们已经知道了差速机器人运动学模型
\begin{cases}\dot{x}=V\cos\theta\\dot{y}=V\sin\theta\\dot{\theta}=\omega\end{cases}
X_e(k+1)=\begin{bmatrix}1&0&-Tv_r\sin\theta_r\0&1&Tv_r\cos\theta_r\0&0&1\end{bmatrix}X_e(k)+\begin{bmatrix}T\cos\theta_r&0\T\sin\theta_r&0\0&T\end{bmatrix}u(k)
# LATEX
## 命令行安装
### 安装
* 安装latex发行版TeX Live
1
sudo apt-get install texlive-full
1
sudo apt-get install texlive-xetex
1
sudo apt-get install texlive-lang-chinese
1
sudo apt-get install texstudio
1
2
3
4
5
6
7
8
9
10
11\documentclass{article}
\usepackage{xeCJK}
\begin{document}
\section{前言}
\section{关于数学部分}
数学、中英文皆可以混排。You can intersperse math, Chinese and English (Latin script) without adding extra environments.
這是繁體中文。
\end{document}1
sudo mkdir /mnt/cdrom
1
sudo mount -o loop ./texlive.iso /mnt/cdrom
1
cd /mnt/cdrom
1
sudo ./install-tl
1
sudo umount -v /mnt/cdrom
1
sudo gedit ~/.bashrc
1
2
3export MANPATH=${MANPATH}:/usr/local/texlive/2024/texmf-dist/doc/man
export INFOPATH=${INFOPATH}:/usr/local/texlive/2024/texmf-dist/doc/info
export PATH=${PATH}:/usr/local/texlive/2024/bin/x86_64-linux1
source ~/.bashrc
1
2cd /usr/share/fonts
mkdir chinese1
sudo mv ~/02_study/Fonts /usr/share/fonts/chinese/
1
fc-list | grep "SimSun"
Q = {q_1, q_2, q_3, …, q_N}
* $V$:所有可能的观测状态的集合:
V={v_1, v_2, v_3, …,v_M}
* $I$:对应的长度为$T$的状态序列
I={i_1, i_2, …, i_T}
* $O$:对应的长度为$T$观察序列
O={o_i, o_2, …, o_T}
* 两个重要假设 * 齐次马尔科夫假设:任意时刻的隐藏状态只依赖于它前一个隐藏状态。如果在时刻$t$的隐藏状态是$i_t=q_i$,在时刻$t+1$的隐藏状态是$i_{i+1}=q_j$,则从时刻$t$到时刻$t+1$的HMM状态转移概率$a_{ij}$可以表示为:
a_{ij}=P(i_{t+1}=q_j|i_t=q_i)
$$
这样$a_{ij}$可以组成马尔科夫链的状态转移矩阵$A$:
$$
A = [a_{ij}]_{N \times N}
$$
-
观测独立性假设:任意时刻的观察状态只仅仅依赖于当前时刻的隐藏状态。如果在时刻的隐藏状态是,而对应的观察状态为,则该时刻观察状态在隐藏状态下生成的概率为,满足:
这样可以组成马尔科夫链的状态转移矩阵:
-
初始隐藏状态概率:
其中
一个HMM模型,可以由隐藏状态初始概率分布,状态转移概率矩阵和观测状态概率矩阵决定。决定状态序列,决定观测序列。因此,HMM模型可以由一个三元组表示如下:
实例
假设我们有3个盒子,每个盒子里都有红色和白色两种球,这三个盒子里球的数量分别是:
| 盒子 | 1 | 2 | 3 |
|---|---|---|---|
| 红球数 | 5 | 4 | 7 |
| 白球数 | 5 | 6 | 3 |
按照下面的方法从盒子里抽球,开始的时候,从第一个盒子抽球的概率是0.2,从第二个盒子抽球的概率是0.4,从第三个盒子抽球的概率是0.4。以这个概率抽一次球后,将球放回。然后从当前盒子转移到下一个盒子进行抽球。规则是:如果当前抽球的盒子是第一个盒子,则以0.5的概率仍然留在第一个盒子继续抽球,以0.2的概率去第二个盒子抽球,以0.3的概率去第三个盒子抽球。如果当前抽球的盒子是第二个盒子,则以0.5的概率仍然留在第二个盒子继续抽球,以0.3的概率去第一个盒子抽球,以0.2的概率去第三个盒子抽球。如果当前抽球的盒子是第三个盒子,则以0.5的概率仍然留在第三个盒子继续抽球,以0.2的概率去第一个盒子抽球,以0.3的概率去第二个盒子抽球。如此下去,直到重复三次,得到一个球的颜色的观测序列:
在这个过程中,观察者只能看到球的颜色序列,不能看到球是从哪个盒子里取出的。
则按照HMM定义:
观测集合为:
状态集合为:
观测序列长度为2,状态序列长度为3。
初始状态分布为:
状态转移概率分布矩阵为:
观测状态概率矩阵为:
求观测序列的概率
我们已知HMM模型的参数,同时我们也已经得到观测序列,现在我们要求观测序列在模型下出现的条件概率。
暴力求解法
首先,任意一个隐藏序列出现的概率是:
对于固定的状态序列,我们要求的观察序列出现的概率是:
则和联合出现的概率是:
然后求边缘概率分布,即可得到观测序列在模型下出现的概率:
虽然上述方法有效,但是如果隐藏状态数非常多,预测状态有种组合,算法复杂度是阶的。
前向算法
前向后向算法是前向算法和后向算法的统称,这两个算法都可以用于求HMM观测序列的概率。
前向算法本质上属于动态规划的算法,也就是我们要通过局部状态递推的公式,然后一步步从子问题的最优解拓展到整个问题的最优解。
前向概率:定义时刻时隐藏状态为,观测状态的序列为的概率为前向概率,记为:
假设在时刻时各个隐藏状态的前向概率,现在我们需要递推出时刻时各个隐藏状态的前向概率。
我们可以基于时刻时各个隐藏状态的前向概率,再乘以对应的状态转移概率,即就是在时刻观测到,并且时刻隐藏状态的概率。对于时刻各个隐藏状态的前向概率进行求和,在时刻的隐藏状态观测到的概率为。
完整步骤如下:
-
计算时刻1的各个隐藏状态前向概率:
-
递推时刻2,3,…,T时刻的前向概率:
-
计算最终结果:
从递推公式可以看出,算法时间复杂度是,比暴力解法的时间复杂度少了几个数量级。
后向算法
后向算法与前向算法十分类似,后向算法用的是“后向概率”。定义时刻时隐藏状态为,从时刻到最后时刻的观测状态的序列为的概率为后向概率,记为:
后向概率的动态规划与前向概率相反。现已找到时刻时各隐藏状态的后向概率,现递推出时刻时各个隐藏状态的后向概率。我们可以计算出观测状态的序列为,时隐藏状态为,时刻隐藏状态为的概率为,接着可以得到观测状态的序列为,t时隐藏状态为,时刻隐藏状态为的概率为,则把所有隐藏状态的概率加起来可以得到观测状态的序列为,时隐藏状态为的概率为,这个概率即为时刻的后向概率。即递推公式如下:
完整步骤如下:
-
计算时刻的各个隐藏状态后向概率:
-
递推时刻时刻的前向概率:
-
计算最终结果:
从递推公式可以看出,算法时间复杂度是。
例子
以前文例子完成一遍前向算法的流程
-
时刻1各个隐藏状态的前向概率:
\begin{eqnarray} \alpha_1(1)&=\pi_1b_1(o_1)=0.2*0.5=0.1 \\ \alpha_1(2)&=\pi_2b_2(o_1)=0.4*0.4=0.16 \\ \alpha_1(3)&=\pi_3b_3(o_1)=0.4*0.7=0.28 \end{eqnarray}
-
时刻2和时刻3
时刻2
\begin{eqnarray} \alpha_2(1)&=(0.1*0.5+0.16*0.3+0.28*0.2)*0.5=0.077 \\ \alpha_2(2)&=(0.1*0.2+0.16*0.5+0.28*0.3)*0.6=0.1104 \\ \alpha_2(3)&=(0.1*0.3+0.16*0.2+0.28*0.5)*0.3=0.0606 \end{eqnarray}
时刻3
\begin{eqnarray} \alpha_3(1)&=(0.077*0.5+0.1104*0.3+0.28*0.2)*0.5=0.04187 \\ \alpha_3(2)&=(0.077*0.2+0.1104*0.5+0.28*0.3)*0.6=0.03551 \\ \alpha_3(3)&=(0.077*0.3+0.1104*0.2+0.28*0.5)*0.3=0.05284 \end{eqnarray}
-
计算最终结果
HMM常用概率的计算
-
给定模型和观测序列在时刻处于状态的概率记为:
利用前向概率和后向概率的定义可知:
于是可以得到:
-
给定模型和观测序列,在时刻处于状态,且时刻处于状态的概率为:
而可以由前向后向概率来表示为:
从而最终我们得到的表达式如下:
-
将和在各个时刻求和可以得到:
在观测序列下状态出现的期望值
在观测序列下由状态转移的期望值
在观测序列下由状态转移到状态的期望值
HMM模型参数求解概述
情况一
我们已知个长度为的观测序列和对应的隐藏状态序列,即是已知的,此时我们可以很容易得最大似然来求解参数。
假设样本从隐藏状态转移到的频率计数是,那么状态转移矩阵求得为:
假设样本隐藏状态为且观测状态为的频率计数是,那么观测状态概率矩阵为:
假设所有样本中初始隐藏状态为的频率计数为,那么初始概率分布为:
情况二
只知道个长度为的观测序列,即是已知的,此时能不能求出合适的HMM模型参数?下面介绍一种名为鲍姆-韦尔奇算法。
原理
鲍姆-韦尔奇算法原理使用的就是EM算法的原理,那么需要在步求出联合分布基于条件概率的期望,其中为当前的模型参数,然后再步最大化这个期望,得到更新的模型参数,接着不停的进行迭代,直到模型参数的值收敛为止。
首先先看看步,当前模型参数为,联合分布基于条件概率的期望表达式为:
在步,我们极大化上式,然后得到更新后的模型参数如下:
通过不断的步和步的迭代,直到收敛。
流程
输入:个观测序列样本
输出:HMM模型参数
-
随机初始化所有的
-
对于每个样本,用前向后向算法计算
-
更新模型参数
-
如果的值已经收敛,则算法结束,否则回到第2步继续迭代。
实验步骤
-
启动小车控制节点
1
2sudo ip link set can0 up type can bitrate 500000
roslaunch scout_base my_car.launch -
启动r3_live节点
1
2
3roslaunch livox_ros_driver livox_lidar_msg.launch
roslaunch realsense2_camera rs_d435_camera_with_model.launch
roslaunch r3live r3live_bag.launch -
录制bag包
1
rosbag record -o test_wheel_0.1.bag /odom /aft_mapped_to_init /cmd_vel
-
轨迹跟踪
1
roslaunch scout_unitree_control scout_tracking.launch
- open_straight
- open_curve
- open_highstraight
- wheel_straight_delay0.1
- wheel_curve_delay0.1
- wheel_highstraight_delay0.1
- wheel_straight_delay0.2
- wheel_highstraight_delay0.2
- Lvio_straight_delay0.2
- Lvio_highstraight_delay0.2
april_odom
-
apriltag_ros::AprilTagDetectionArray消息类型
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24std_msgs/Header header
uint32 seq
time stamp
string frame_id
apriltag_ros/AprilTagDetection[] detections
int32[] id
float64[] size
geometry_msgs/PoseWithCovarianceStamped pose
std_msgs/Header header
uint32 seq
time stamp
string frame_id
geometry_msgs/PoseWithCovariance pose
geometry_msgs/Pose pose
geometry_msgs/Point position
float64 x
float64 y
float64 z
geometry_msgs/Quaternion orientation
float64 x
float64 y
float64 z
float64 w
float64[36] covariance
其他
工控机各种库的版本
查看ros版本命令roscore,ros版本noetic。
查看pcl版本命令dpkg -l libpcl-dev,pcl版本1.8.1。
查看eigen3版本命令dpkg -s libeigen3-dev | grep 'Version',eigen3版本3.3.4。
查看opencv版本命令pkg-config --modversion opencv,opencv版本
报错记录
报错一
**描述:**使用eigen库中求逆运算时报错
1 | undefined reference to `Eigen::MatrixBase<Eigen::Matrix<double, 2, 2, 0, 2, 2> >::inverse() const' |
**原因:**头文件引用错误
解决:
1 | #include <Eigen/LU> |

