文档维护：Arvin

网页部署：Arvin

▶

写在前面：本文内容是作者在深蓝学院自动驾驶预测与决策规划学习时的笔记，作者按照自己的理解进行了记录，如果有错误的地方还请执政。如涉侵权，请联系删除。

时空联合规划

传统的时空分离规划只考虑了路径规划和速度规划，分别对应横向控制和纵向控制。而时空联合规划算法则同时考虑空间和时间来规划轨迹，在路径基础上再求解速度从而形成轨迹，能够能直接在$x-y-t$（即平面和时间）三个维度的空间中直接求解最优轨迹。

时空分离规划：

$1$

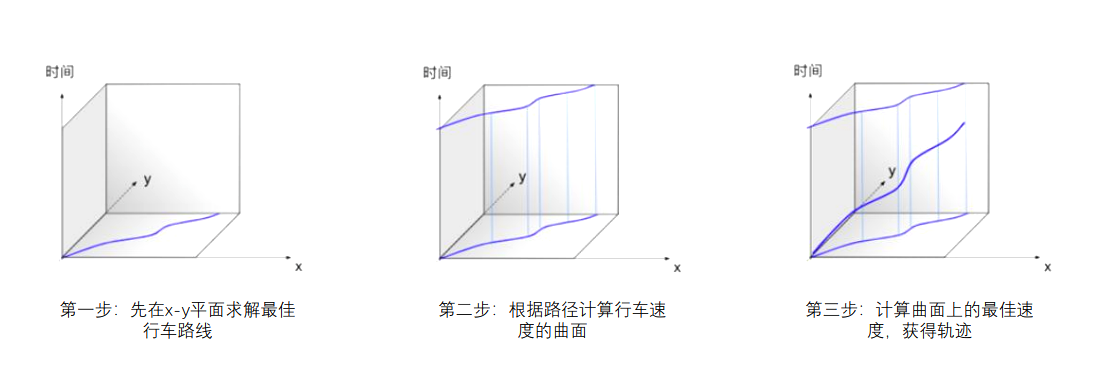
时空联合规划：

$2$

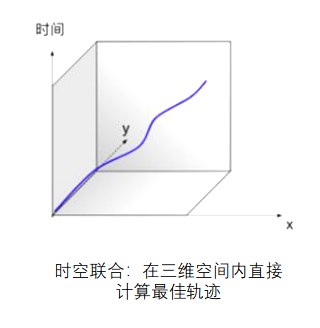
基于搜索（Hybrid A*）的时空联合规划方法

构建三维时空联合规划地图

构建二维栅格地图

二维x-y栅格地图只具有几何属性，无法直接搜索带有时间属性的可行驶轨迹。

（灰色圆形区域部分：在最大转向角下也会发生碰撞或不可能到达目的地；

半径大小：最小转弯半径；

方向：车速方向相切；）

$3$
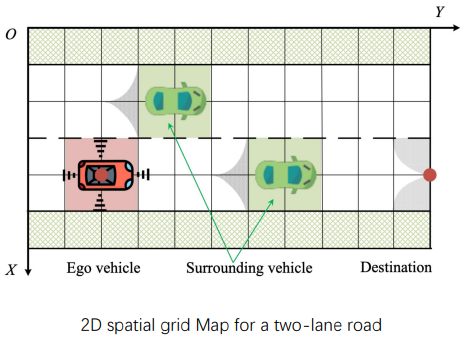
沿时间轴扩展生成三维时空地图

如下图所示，多个地图层相互平行；相邻图层中的两个状态根据时间步长由有向边相连；蓝色有向边连接的点序列表示以$\Delta t$为时间步长离散化的时空轨迹；绿色部分：动态障碍物在$\Delta t$为时间步长离散化的位置（由轨迹预测模块给出）

$4$

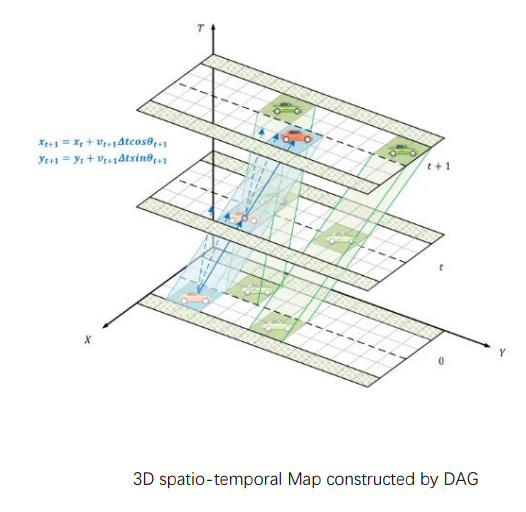
三维时空地图中包含了如下信息：

车辆位置状态信息
车辆运动学信息：
- 蓝色有向线段在X-O-T平面的投影斜率为横向速度。
- 蓝色有向线段在Y-O-T平面的投影斜率为纵向速度。
- 蓝色有向线段在X-O-Y平面的投影倾斜角为偏航角
根据相邻状态可以计算动作空间
根据动作空间扩展时空地图（图中由蓝色实线、虚线所示）

基于Hybrid A*的时空节点扩展

$5$

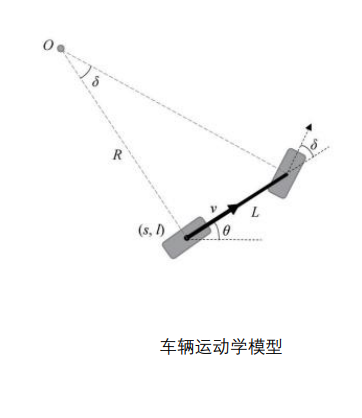
离散化前轮转角集合$\Delta$ ：

$\Delta=\left\{\delta_i\mid-\delta_{max}+(i-1)\cdot\frac{\delta_{max}-(-\delta_{max})}{N-1}\right\}$

其中$\delta_i$为离散后的前轮转角。

离散加速度集合$A$：

$A=\{-\mathrm{a}_{max},...,0,...,\mathrm{a}_{max}\}$

状态更新方程：

$\begin{cases}s_i=s_p+v_p\cdot dt\cdot cos\theta_i\\l_i=l_p+v_p\cdot dt\cdot sin\theta_i\\\theta_i=\theta_p+v_i\cdot dt\cdot tan\delta_i/L\\v_i=v_p+a_i\cdot dt\\t_i=t_p+dt\end{cases}$

上面是将车辆运动连续动作根据运动学模型离散化，接下来进行Hybrid A的算法设计（Hybrid A算法原理参阅之前文章）

设计启发函数
$H_{i}=w_{H1}\cdot\sqrt{(s_{\text{goal}}-s_{i})^{2}+(l_{\text{goal}}-l_{i})^{2}}+w_{H2}\cdot(t_{\text{goal}}-t_{i})$
其中$s_{goal}、l{goal}$分别是目标节点的纵向、横向位置。$t_{goal}$为目标节点对应的相对时间，避免陷入时间停滞，加快搜索过程；$w_{H1}$与$w_{H2}$是对应权重。
设计成本函数
$G_{i}=G_{p}+w_{g1}\cdot E_{i}+w_{g2}\cdot C_{i}+w_{g3}\cdot S_{i}$
其中$G_p$为父节点成本，$w_{g1},w_{g2},w_{g3}$为权重系数。

$E_i$为子节点目标代价：
$E_i=|\mathrm v_i-\mathrm v_{\mathrm expected}|$
$C_i$为子节点舒适性代价：
$C_i=|l_i-l_{centerline}|$
$S_i$为子节点安全性代价：
$S_i=R(s,l)\cdot\exp(\cos\theta_r)$ $R(s,l)=\exp\left[-\frac{1}{2}\times\left(\frac{(s-u_s)^2}{\sigma_{sg}^2}+\frac{(l-u_l)^2}{\sigma_{lg}^2}\right)\right]$ $r=(s-u_s,l-u_l)$
$(s,l),(u_l,u_s)$分别表示节点和障碍物的位置；$\sigma_{sg},\sigma_{lg}$分别表示障碍物在$s$向、$l$向的权重系数；$r$为节点相对于障碍物的位置向量；$\theta+r$为向量$r$与障碍物速度$v$之间的夹角。

算法流程：

以当前自车所在位置$(s_{1},l_{1},\theta_{1},v_{1},t_{1})$为起点进行时空节点扩展；
扩展过程中考虑节点无碰撞和道路边界约束问题进行检查；
通过节点代价评估寻找最优扩展节点，直至达到目标节点；
通过各个最优节点得到初始粗轨迹。

$6$

基于迭代的时空联合规划方法

由于时空联合规划方法加上了时间的维度，因此基于搜索的方法搜索的轨迹空间十分庞大。减少时间和空间上的搜索复杂度，使规划聚焦于最优解可能出现的区域。

基于时空走廊的规划方法

参考文献：Multipolicy and Risk-aware Contingency Planning for Autonomous Driving

在高度交互的环境中完成安全和高效的规划任务是一项具有挑战的任务，这是由于交通参与者的随机性以及它们与自车的隐式互动，无法直接观测它们的多模态的意图。对于这种交互决策问题，一般有两种主流方法：第一种是马尔可夫决策过程（MDP：Markov decision process）和部分可观察马尔可夫决策过程（POMDP： partially observable Markov decision process），这种方法存在一个缺点，随着问题规模的增加（也就是参与交互的障碍物越多），计算量剧增；为了减少计算量，可以使用规则进行剪枝，将原始问题分解成有限数量的闭环策略评估。然而，剪枝的缺点是，很难设计出好的规则去适应所有的场景。

第二种方法是数值优化方法（如：contigency planning），它是在运动规划层为多种可能的未来生成应急计划。通过优化树状（tree-structured）轨迹来处理环境不确定性，其中每个分支都好考虑了潜在的风险，但contigency planning 对周围障碍物的选择是一个问题。

而为了解决上述问题，MARC算法，结合前面两种方法的优点，将行为和运动规划层进行组合。首先利用前向模拟（Forward Simulations）生成基于语义级别的关键场景集（具有动态分支点的场景树，使用分叉点减少相同部分的计算量），然后使用Risk-aware Contiency Planning(使用线性规划器LP和迭代线性二次调节器iLQR)进行优化，生成考虑多样化风险和未来场景的轨迹树，最后进行cost计算，选择出合适的场景和轨迹。

语义时空走廊（Semantic Spatio-Temporal Semantic Corridor）一系列被语义要素约束的相互连接的无碰撞立方体。

$7$

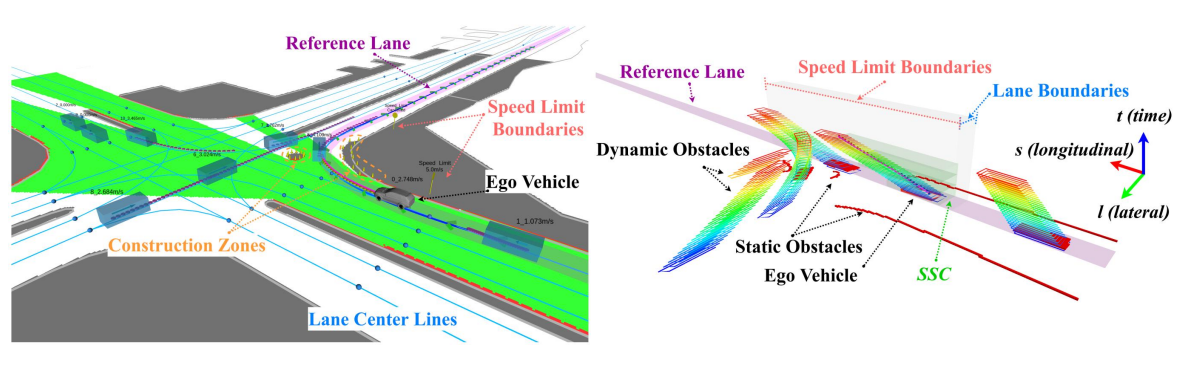
环境理解：处理规划所需要的语义要素（占据栅格地图、动态物体、车道线、交通规则）；
预测：提供移动物体的未来轨迹；
行为规划：假设所有车辆执行有限的闭环策略（车道保持，左变道，右变道）；使用简化模型模拟所有车辆的未来状态；根据代价函数评估未来的局面，选择最优的行为；
运动规划：时空语义走廊生成/轨迹优化。

语义时空走廊构建

$8$

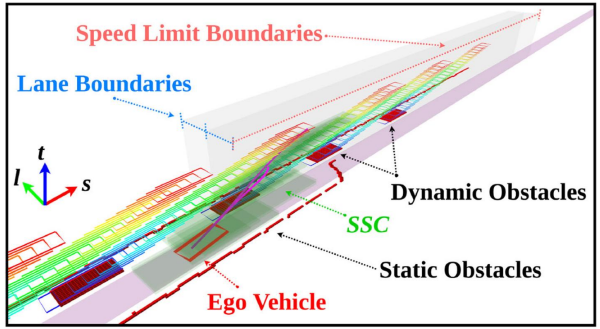
障碍物要素：

坐标系：$s-l-t$3D构型空间（Recall：用于搜索的$s-l-t$栅格地图）
静止障碍物：横跨整个时间轴的障碍物
动态障碍物：根据预测轨迹在时间轴上存在的一系列障碍物
红灯：占据特定纵向空间和时间的障碍物

约束要素：

速度约束：道路限速，停止标志
时间约束：变道时长
软约束与硬约束
语义边界的概念：特定语义约束开始和停止生效的位置，例如速度约束的纵向范围$[s_{begin}, s_{end}]$，变道时长约束的横向范围$[d_{begin}, d_{end}]$

输入数据：

其他车辆的未来状态（MPDM前向模拟）
自车初始状态
语义边界
$s-l-t$构型空间

时空走廊轨迹轨迹规划

种子生成

将前向模拟状态投影至$s-l-t$坐标系，初始立方体由连续两个种子作为顶点构成，初始立方体需保证无碰撞，并且保证时空拓扑的一致。

$9$
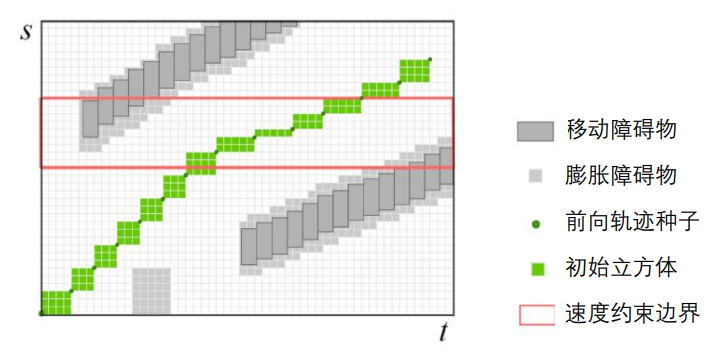
膨胀立方体

将第一个立方体膨胀至语义边界和障碍物。

$10$
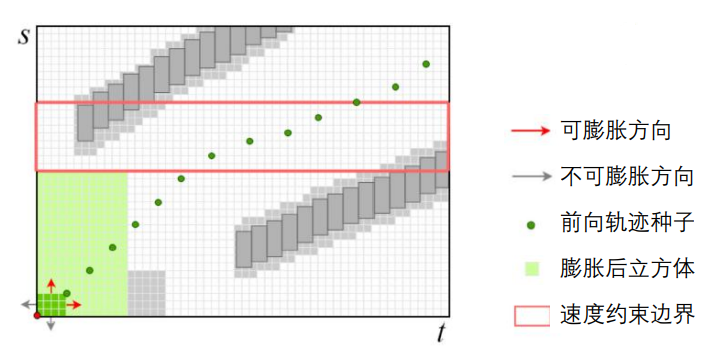
关联约束

$11$
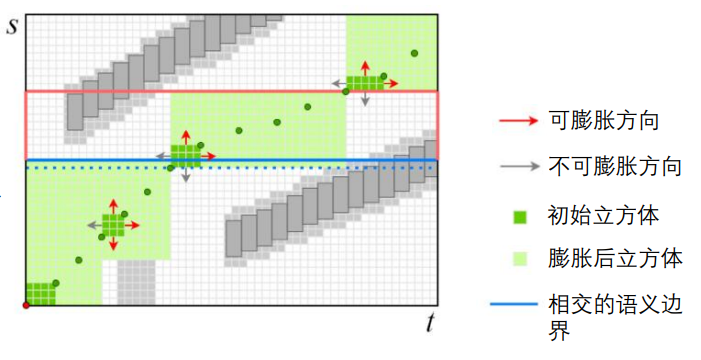
放宽边界

考虑软约束，留出额外的空间，并且保留硬约束与避障。

$12$

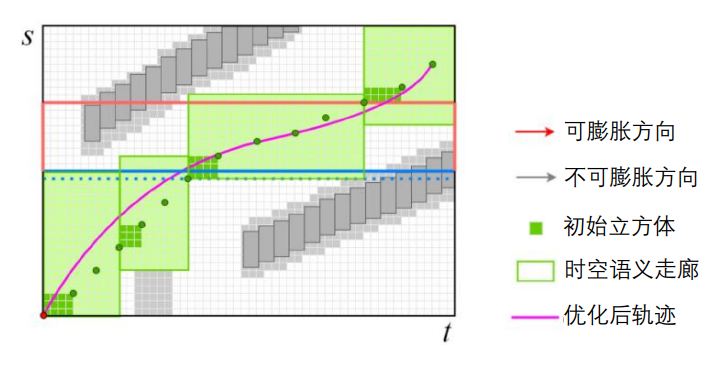
其中具体的方法

保证安全性和可行性的轨迹生成
轨迹表示

每个时空走廊中的立方体对应着一段贝塞尔曲线，每个维度$\sigma \in \{s,l\}$各用一条n段的贝塞尔轨迹表示，$p_i^j$对应着第$j$段轨迹的第$i$个控制点，$t_0,t_1,…,t_n$是每段轨迹的初始和末尾时刻，使用尺度因子$\alpha_j$保证轨迹定义在$[0, 1]$的区间上
$\begin{aligned}&\alpha_{1}\cdot\sum_{i=0}^{m}p_{i}^{1}\cdot b_{m}^{i}\left(\frac{t-t_{0}}{\alpha_{1}}\right),t\in[t_{0},t_{1}]\\&f^{\sigma}(t)=\begin{cases}&\alpha_{2}\cdot\sum_{i=0}^{m}p_{i}^{2}\cdot b_{m}^{i}\left(\frac{t-t_{1}}{\alpha_{2}}\right),t\in[t_{1},t_{2}]\\&\vdots\\&\alpha_{n}\cdot\sum_{i=0}^{m}p_{i}^{n}\cdot b_{m}^{i}\left(\frac{t-t_{n-1}}{\alpha_{n}}\right),t\in[t_{n-1},t_{n}]\end{cases}\end{aligned}$
轨迹优化（QP问题）

最小化jerk，目标函数：

约束:
- 利用凸包性质得到的安全和动力学约束，$\beta_{j,-}^{\sigma,(k)},\beta_{j,+}^{\sigma,(k)}$表示第j段轨迹k阶导数的上下界
  $\beta_{j,-}^{\sigma,(k)}\leq\frac{d^{k}f_{j}^{\sigma}(t)}{dt^{k}}\leq\beta_{j,+}^{\sigma,(k)},\sigma\in\{s,l\},k=0,1,2$
- 首末状态约束
  $\frac{d^kf_0^\sigma(t_0)}{dt^k}=\sigma_{t_0}^{(k)},\frac{d^kf_n^\sigma(t_n)}{dt^k}=\sigma_{t_n}^{(k)}$
- 连续性约束
  $\frac{d^kf_j^\sigma(t_j)}{dt^k}=\frac{d^kf_{j+1}^\sigma(t_j)}{dt^k}$

参考代码：https://github.com/HKUST-Aerial-Robotics/EPSILON/blob/master/util/ssc_planner/src/ssc_planner/ssc_planner.cc