机器人中的数值优化（一）

文档维护：Arvin

网页部署：Arvin

▶

写在前面：本文内容是作者在深蓝学院机器人中的数值优化学习时的笔记，作者按照自己的理解进行了记录，如果有错误的地方还请执政。如涉侵权，请联系删除。

凸优化基础

最优化问题概括

最优化问题一般可以描述为：

$$\begin{array}{rl}\min&f(x)\\\mathrm{s.t.}&g(x)\leq0\\&h(x)=0\end{array}$$

凸集合与凸函数

凸集

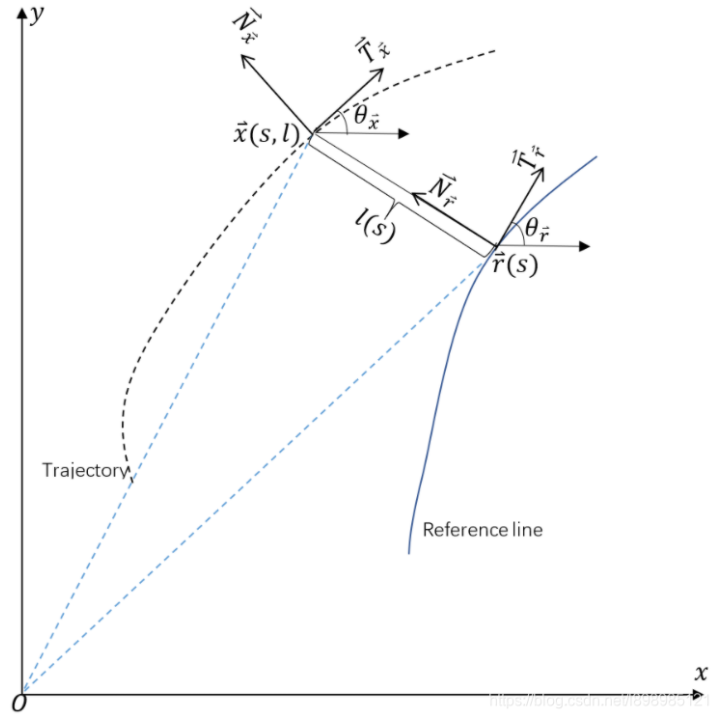
对于$\mathbb{R}^{n}$中的两个点$x_{1}\ne x_{2}$，形如$y=\theta x_{1}+(1-\theta) x_{2}$的点形成了过点$x_{1}$和$x_{2}$的直线。当$0\le \theta \le1$，这样的点形成了连接点的$x_{1}$和$x_{2}$的线段。

---

定义：如果过集合C中任意两点的直线都在C内，则成C为放射集，即

$$\theta x_{1}, x_{2} \in C \Longrightarrow \theta x_{1}+(1-\theta) x_{2} \in C, \forall \theta \in \mathbb{R}$$

线性方程组$Ax=b$的解集是仿射集。反之，任何仿射集都可以表示成一个线性方程组的解。

---

定义：如果连接集合C中任意两点的线段都在C内，则称C为凸集，即

$$x_{1}, x_{2} \in C \Longrightarrow \theta x_{1}+(1-\theta) x_{2} \in C, \forall 0 \leqslant \theta \leqslant 1$$

---

从凸集可以引出凸组合和凸包等概念，形如

$$\begin{array}{r} x=\theta_{1} x_{1}+\theta_{2} x_{2}+\cdots+\theta_{k} x_{k} \\ 1=\theta_{1}+\theta_{2}+\cdots+\theta_{k}, \quad \theta_{i} \geqslant 0, i=1,2, \cdots, k \end{array}$$

的点称为$x_{1},x_{2},…,x_{k}$的凸组合。集合S中点所有可能的凸组合构成的集合称为S的凸包，记作conv S是包含S的最小凸集。如下图所示，左边为离散点集的凸包，右边为扇形的凸包：

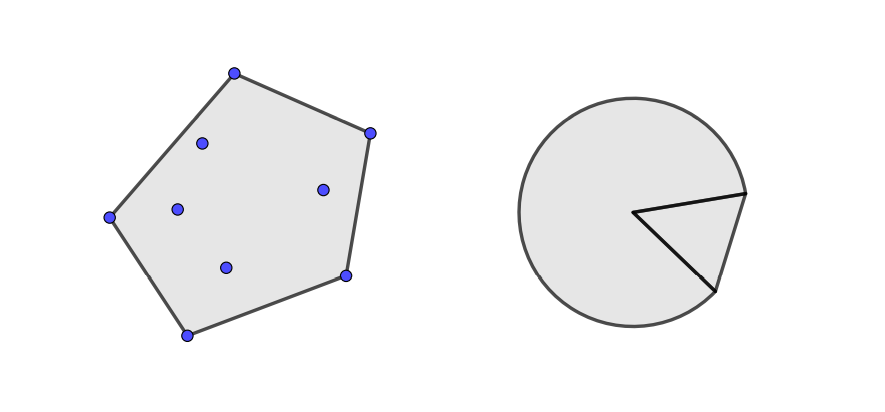
若在凸组合的定义中去掉$\theta_{i}\ge 0$的限制，可以得到仿射包的概念。

如下图所示，展示了$ \mathbb{R}^{3}$中圆盘S的仿射包，其为一个平面：

---

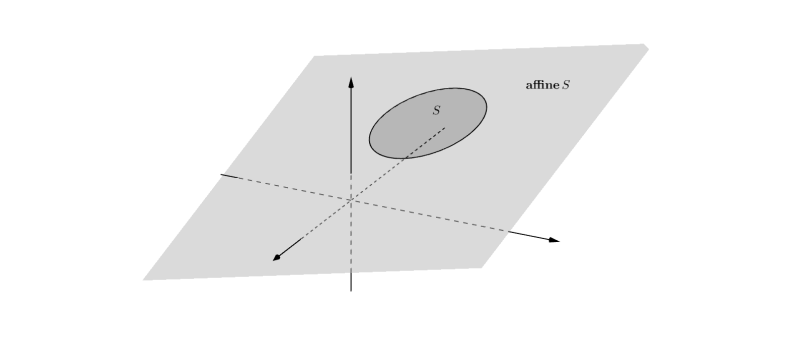
定义：（仿射包）设S为$\mathbb{R}$的子集，称如下集合为S的仿射包：$\left\{x \mid x=\theta_{1} x_{1}+\theta_{2} x_{2}+\cdots+\theta_{k} x_{k}, \quad x_{1}, x_{2}, \cdots, x_{k} \in S, \quad \theta_{1}+\theta_{2}+\cdots+\theta_{k}=1\right\}$，记为affine S。

---

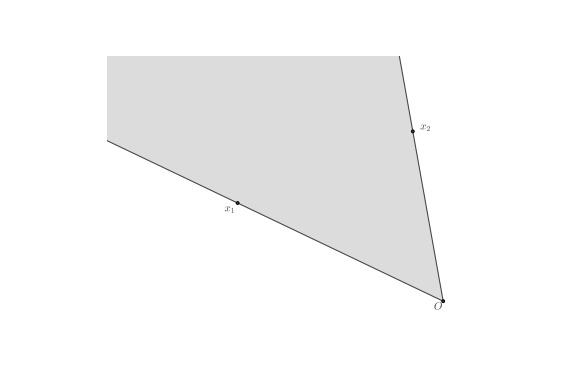
形如$x=\theta_{1} x_{1}+\theta_{2} x_{2}, \quad \theta_{1}>0, \theta_{2}>0$的点称为点$x_{1},x_{2}$的锥组合，若集合S中任意点的锥组合都在S中，则称S为凸锥，如下图所示：

高阶函数

• 函数（Function）：

$$f(x)=f(x_1,x_2,x_3)$$

• 梯度（Gradient）：

$$\nabla f(x)=\begin{pmatrix}\partial_1f(x)\\\partial_2f(x)\\\partial_3f(x)\end{pmatrix}$$

$Let f(x):Rn→R\mathrm{Let~}f(x):\mathbb{R}^n\to\mathbb{R}$，梯度向量包含所有一阶偏导数：

$$\nabla f(x)=\frac{df}{dx}=\begin{pmatrix}\frac{\partial f}{\partial x_1}\\\frac{\partial f}{\partial x_2}\\\vdots\\\frac{\partial f}{\partial x_n}\end{pmatrix}$$

该矢量指示最陡上升的方向。因此，向量 $-\nabla f(x)$ 表示该点的函数最速下降的方向。

• 海森矩阵（Hessian）：

$$\nabla^2f(x)=\begin{pmatrix}\partial_1^2f(x)&\partial_1\partial_2f(x)&\partial_1\partial_3f(x)\\\partial_2\partial_1f(x)&\partial_2^2f(x)&\partial_2\partial_3f(x)\\\partial_3\partial_1f(x)&\partial_3\partial_2f(x)&\partial_3^2f(x)\end{pmatrix}$$

$\mathrm{Let~}f(x):\mathbb{R}^n\to\mathbb{R}$，海森矩阵包含所有二阶偏导数：

$$f^{\prime\prime}(x)=\frac{d(\nabla f)}{dx^T}=\frac{d\left(\nabla f^T\right)}{dx}=\begin{pmatrix}\frac{\partial^2f}{\partial x_1\partial x_1}&\frac{\partial^2f}{\partial x_1\partial x_2}&\cdots&\frac{\partial^2f}{\partial x_1\partial x_n}\\\frac{\partial^2f}{\partial x_2\partial x_1}&\frac{\partial^2f}{\partial x_2\partial x_2}&\cdots&\frac{\partial^2f}{\partial x_2\partial x_n}\\\vdots&\vdots&\ddots&\vdots\\\frac{\partial^2f}{\partial x_n\partial x_1}&\frac{\partial^2f}{\partial x_n\partial x_2}&\cdots&\frac{\partial^2f}{\partial x_n\partial x_n}\end{pmatrix}$$

但实际上，Hessian 可以是这样的张量： $(f(x):\mathbb{R}^n\to\mathbb{R}^m)$ 只是 3d 张量，每个切片只是对应的 hessian标量函数$\left(H\left(f_{1}(x)\right),H\left(f_{2}(x)\right),\ldots,H\left(f_{m}(x)\right)\right)$。

• 雅可比矩阵（Jacobian）：

多维梯度的推广：$f(x):\mathbb{R}^n\to\mathbb{R}^m$

$$\left.f'(x)=\frac{df}{dx^T}=\left(\begin{array}{cccc}\frac{\partial f_1}{\partial x_1}&\frac{\partial f_1}{\partial x_2}&\cdots&\frac{\partial f_1}{\partial x_n}\\\frac{\partial f_2}{\partial x_1}&\frac{\partial f_2}{\partial x_2}&\cdots&\frac{\partial f_2}{\partial x_n}\\\vdots&\vdots&\ddots&\vdots\\\frac{\partial f_m}{\partial x_1}&\frac{\partial f_m}{\partial x_2}&\cdots&\frac{\partial f_m}{\partial x_n}\end{array}\right.\right)$$

• 泰勒展开：

$$f(x)=f(0)+x^T\nabla f(0)+\frac12x^T\nabla^2f(0)x+O\Big(\left\|x-x_0\right\|^3\Big)$$

事实上，我们可以将海森矩阵看作梯度的雅可比。

凸函数

定义：（凸函数）设函数$f$为适当函数，如果dom $f$是凸集，且

$$f(\theta x+(1-\theta) y) \leqslant \theta f(x)+(1-\theta) f(y)$$

对所有$x, y \in \operatorname{dom} f, 0 \leqslant \theta \leqslant 1$，则称$f$为凸函数。

直观地来看，连接凸函数的图像上任意两点的线段都在函数图像上方。

梯度下降法

原理

梯度下降法其原理可用公式进行表示：

$$\begin{array}{l} x^{k+1}=x^{k}+\tau d \\ d=-\nabla f\left(x^{k}\right) \end{array}$$

这是一个迭代公式：其中$\tau$表示搜索步长，$d$表示搜索方向即负梯度方向。步长的设定通常会采用如下几种方法：

• 恒定步长（Constant step size）:

  $$\tau = c$$

• 递减步长（Diminishing step size）：

  $$\tau = c/k$$

• 步长的精确搜索（Exact line search）：

  $$\tau=\arg \min _{\alpha} f\left(x^{k}+\alpha d\right)$$

• 步长的非精确搜索（Inexact line search）：

  $$\tau \in\left\{\alpha \mid f\left(x^{k}\right)-f\left(x^{k}+\alpha d\right) \geq-c \cdot \alpha d^{\mathrm{T}} \nabla f\left(x^{k}\right)\right\}$$

主要讲述一下步长的精确搜索和不精确搜索。

步长的精确搜索

若我们已经知道了一个下降方向$d_{k}$，就只需要求参数$\alpha$使其满足一维优化问题$\min f\left(x^{k}+\alpha d\right)$的解，令$\phi(\alpha)=f\left(x_{k}+\alpha d_{k}\right)$，则$\phi^{\prime}(\alpha)=\nabla f\left(x_{k}+\alpha d_{k}\right)^{T} d_{k}=0$，求解该线性方程组即可。对于简单的方程，精确搜索是非常快速有效的。但是当目标函数比较复杂或维度比较高时，每次求解步长将会非常耗时。因此我们往往采用非精确搜索的方法。

步长的非精确搜索

步长的非精确搜索一般按照Armijo搜索条件去搜索。Armijo条件（充分减少条件）：

$$\tau \in\left\{\alpha \mid f\left(x^{k}\right)-f\left(x^{k}+\alpha d\right) \geq-c \cdot \alpha d^{\mathrm{T}} \nabla f\left(x^{k}\right)\right\}$$

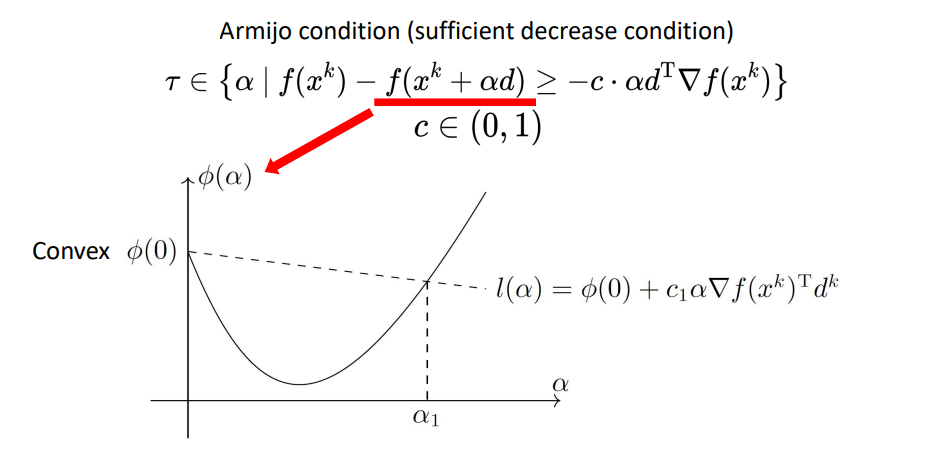
利用步长的非精确搜索方法，其伪代码如下：

1. 给定最初点$x^{1}$，给定初始步长$\tau$，设置允许误差$\theta > 0$，迭代次数k=1
2. 计算梯度作为搜索方向：$d^{k} = -\nabla f\left(x^{k}\right)$
3. 根据Armijo条件更新步长：如果$f\left(x^{k}+\tau d\right)>f\left(x^{k}\right)+c \cdot \tau d^{T} \nabla f\left(x^{k}\right)$，则$\tau \leftarrow \tau / 2$直到满足Armijo条件为止。
4. 进行迭代：$x^{k+1}=x^{k}+\tau d$
5. 若精度达到误差要求迭代结束，否则转到步骤2

修正阻尼牛顿法

通过二阶泰勒展开：

$$f(\boldsymbol{x})\approx\hat{f}\left(\boldsymbol{x}\right)\triangleq f(\boldsymbol{x}_k)+\nabla f(\boldsymbol{x}_k)^T(\boldsymbol{x}-\boldsymbol{x}_k)+\frac12(\boldsymbol{x}-\boldsymbol{x}_k)^T\nabla^2f(\boldsymbol{x}_k)(\boldsymbol{x}-\boldsymbol{x}_k)$$

最小化二次近似：

$$\begin{aligned}&\nabla\hat{f}\left(\boldsymbol{x}\right)=\nabla^2f(\boldsymbol{x}_k)(\boldsymbol{x}-\boldsymbol{x}_k)+\nabla f(\boldsymbol{x}_k)=\mathbf{0}\\&\Longrightarrow\boldsymbol{x}=\boldsymbol{x}_k-\left[\nabla^2f(\boldsymbol{x}_k)\right]^{-1}\nabla f(\boldsymbol{x}_k)\end{aligned}$$

规定：

$$\nabla^2f(\boldsymbol{x}_k)\succ\boldsymbol{O}$$

牛顿步长：

$$\boldsymbol{x}_{k+1}=\boldsymbol{x}_k-\left[\nabla^2f(\boldsymbol{x}_k)\right]^{-1}\nabla f(\boldsymbol{x}_k)$$

其伪代码如下：

initialization $x\gets\boldsymbol{x}_0\in\mathbb{R}^n$

while $|\nabla f(\boldsymbol{x})|>\delta$ do

​ $\boldsymbol{d}\gets-\boldsymbol{M}^{-1}\nabla f(\boldsymbol{x})$

​ $t\gets$ backtracking line search

​ $x\gets x+td$

end while

return

作业

要求

使用 Armijo condition 实现线搜索最陡梯度下降。

目标函数为Rosebrock函数：

$$f(\mathbf{x})=f(x_1,x_2,\ldots,x_N)=\sum_{i=1}^{N/2}\Bigl[100\Bigl(x_{2i-1}^2-x_{2i}\Bigr)^2+(x_{2i-1}-1)^2\Bigr]$$

结果

具体代码见：https://github.com/arvinzyj/Optimization-in-Robotic/tree/main/chapter01

2维

• 首先设置维度和初始点：2, [2, 2]
• 然后运行

python demo01.py

• 输出结果

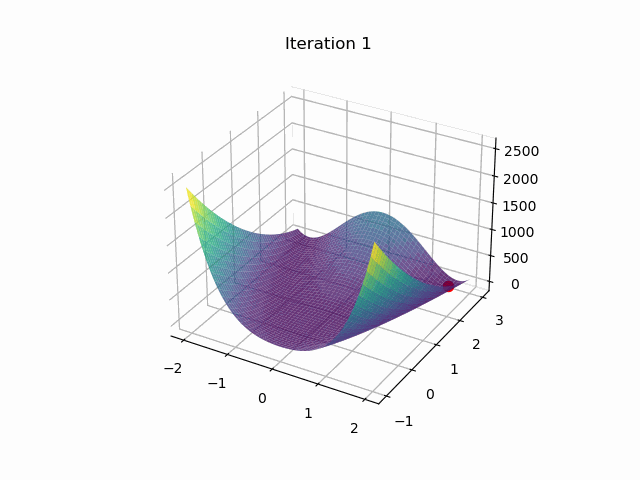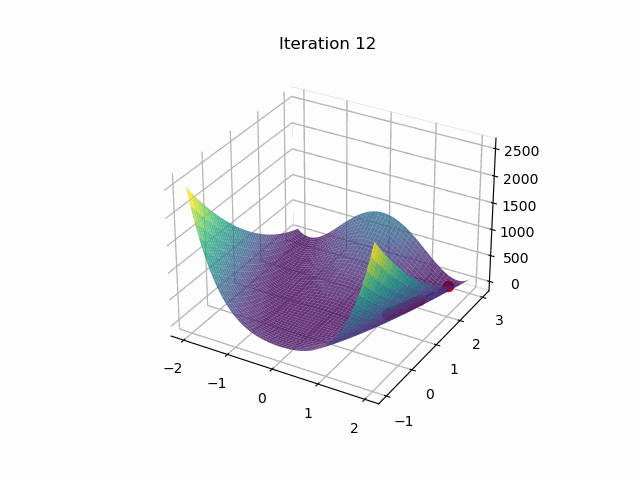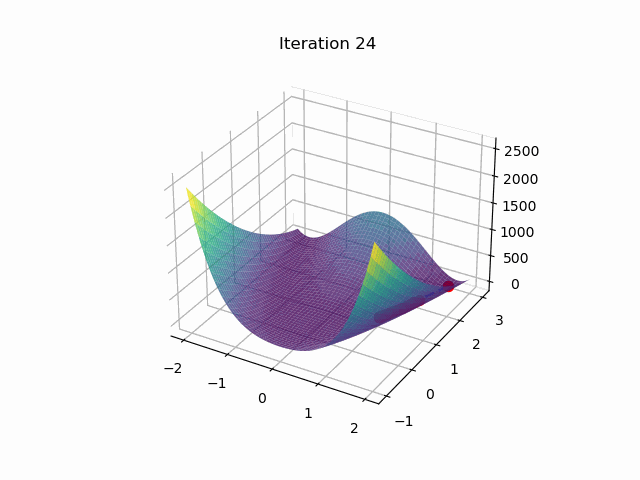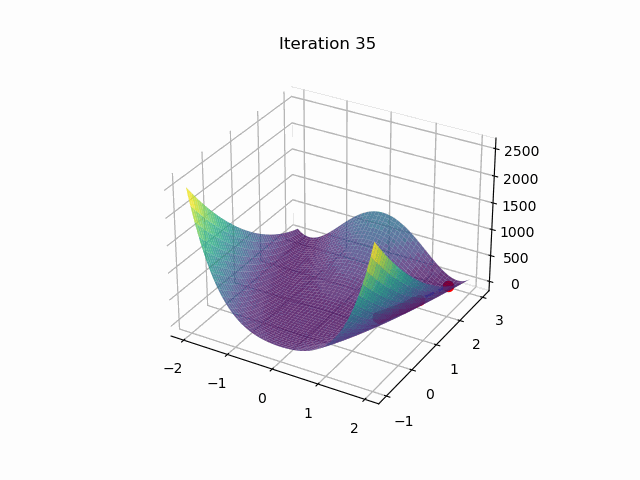
最后结果：

迭代次数：33997

位置：[1.00111873349992 1.00224319227457]

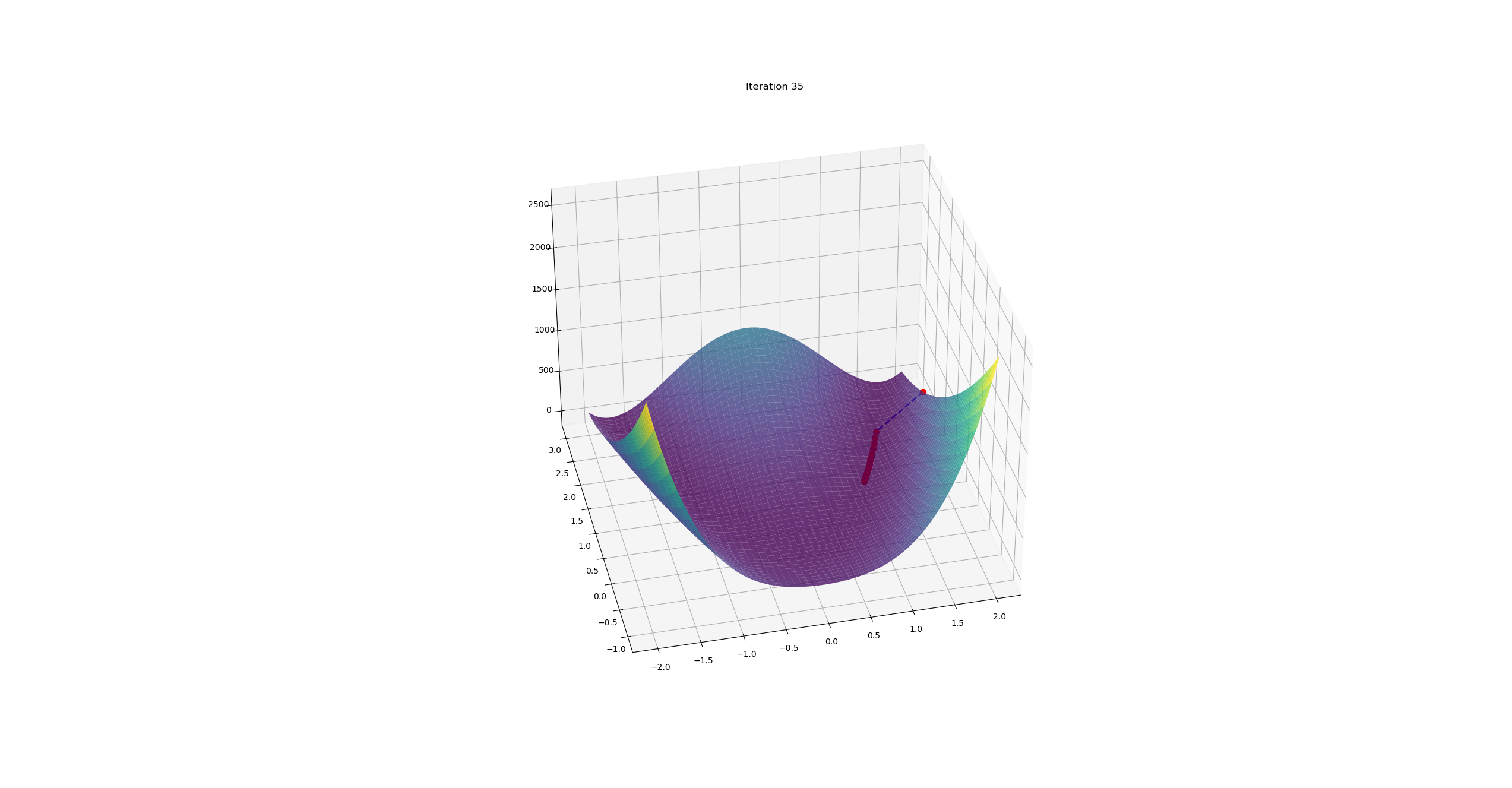
2n维

• 首先设置维度和初始点：4, [2, 2， 2， 2]
• 然后运行

python demo01.py

• 输出结果

最后结果：

迭代次数：35737

位置：[1.00079076283692 1.00158531378990 1.00079076283692 1.00158531378990]