李群李代数（一）

文档维护：Arvin

网页部署：Arvin

▶

写在前面：这篇的内容主要来自于《slam十四讲：从入门到实践》中的第三、四章，是为了引出李群李代数，文章大多记录了一些结论，如果对推导有兴趣可以去看书中详细的过程。

基础知识

三维空间刚体运动

旋转矩阵

1.反对称矩阵

设$A=(a_{ij})_{n \times n}$，若其中元素满足$a_{ij}=a_{ji},\forall i,j\Leftrightarrow A^T=A$，则称$A$是对称矩阵；若其元素满足$a_{ij}=-a_{ji},\forall i,j\Leftrightarrow A^T=-A$，则称$A$为反对称矩阵。

若$A$是反对称矩阵，则$a_{ij}=-a_{ij}$，当$i=j$时，便有$a_{ij}=0$，即反对称矩阵对角线上的元全为零，而位于主对角线两侧对称的元素反号。

2.旋转矩阵

欧氏变换由旋转和平移组成。我们首先考虑旋转。设某个单位正交基$(e_1, e_2, e_3)$经过一次旋转变成了$(e^{\prime}_1, e^{\prime}_2, e^{\prime}_3)$。那么，对于同一个向量$a$，它在两个坐标系下的坐标分别为$[a_1, a_2, a_3]^T$和$[a^{\prime}_1, a^{\prime}_2, a^{\prime}_3]^T$。有：

$$\symbfit{a}=[\boldsymbol{e}_1,\boldsymbol{e}_2,\boldsymbol{e}_3]\begin{bmatrix}a_1\\\\a_2\\\\a_3\end{bmatrix}=[\boldsymbol{e}_1',\boldsymbol{e}_2',\boldsymbol{e}_3']\begin{bmatrix}a_1'\\\\a_2'\\\\a_3'\end{bmatrix}$$

左乘$\begin{bmatrix}e_1^\mathrm{T}\\e_2^\mathrm{T}\\e_3^\mathrm{T}\end{bmatrix}$，得到：

$$\begin{bmatrix}a_1\\a_2\\a_3\end{bmatrix}=\begin{bmatrix}e_1^{\mathrm{T}}e_1'&e_1^{\mathrm{T}}e_2'&e_1^{\mathrm{T}}e_3'\\e_2^{\mathrm{T}}e_1'&e_2^{\mathrm{T}}e_2'&e_2^{\mathrm{T}}e_3'\\e_3^{\mathrm{T}}e_1'&e_3^{\mathrm{T}}e_2'&e_3^{\mathrm{T}}e_3'\end{bmatrix}\begin{bmatrix}a_1'\\a_2'\\a_3'\\a_3'\end{bmatrix}\overset{\mathrm{def}}{\operatorname*{=}}\boldsymbol{R}\boldsymbol{a}'$$

我们称$R$为旋转矩阵，也叫做方向余弦矩阵。

旋转矩阵是一个行列式为1的正交矩阵。反之，行列式为1的正交矩阵也是一个旋转矩阵。所以，可以将$n$维旋转矩阵的集合定义如下：

$$\mathrm{SO}(n)=\{\boldsymbol{R}\in\mathbb{R}^{n\times n}|\boldsymbol{R}\boldsymbol{R}^\mathrm{T}=\boldsymbol{I},\det(\boldsymbol{R})=1\}$$

$SO(n)$是一个特殊正交群。

3.变换矩阵

欧式变换中，除了旋转还有平移。用公式表示：

$$\boldsymbol{a'}=\boldsymbol{Ra}+\boldsymbol{t}$$

其中$R$为旋转矩阵，$t$为平移向量。但若经过多次变换，这里并非完全线性关系，如：

$$b=R_1\boldsymbol{a}+\boldsymbol{t}_1,\quad c=\boldsymbol{R}_2\boldsymbol{b}+\boldsymbol{t}_2$$ $$c=R_2\left(R_1\boldsymbol{a}+\boldsymbol{t}_1\right)+\boldsymbol{t}_2$$

为了化简，我们引入齐次坐标和变换矩阵：

$$\begin{bmatrix}a'\\\\1\end{bmatrix}=\begin{bmatrix}R&t\\\mathbf{0}^\mathrm{T}&1\end{bmatrix}\begin{bmatrix}a\\\\1\end{bmatrix}\overset{\mathrm{def}}{\operatorname*{=}}T\begin{bmatrix}a\\\\1\end{bmatrix}$$

在一个三维向量的末尾添加1，将其变成四维矩阵，成为齐次坐标。矩阵$T$成为变换矩阵。这种矩阵又被称为特殊欧式群：

$$\mathrm{SE}(3)=\left\{\boldsymbol{T}=\begin{bmatrix}\boldsymbol{R}&t\\\boldsymbol{0}^\mathrm{T}&1\end{bmatrix}\in\mathbb{R}^{4\times4}|\boldsymbol{R}\in\mathrm{SO}(3),\boldsymbol{t}\in\mathbb{R}^3\right\}$$

旋转向量和欧拉角

1.旋转向量

任意旋转都可以用一个旋转轴和一个旋转角来刻画。我们使用一个向量，其方向与旋转轴一致，而长度等于旋转角，这种向量称为旋转向量。

假设有一个旋转矩阵$R$。假设旋转轴为一个单位长度的向量$n$，角度为$\theta$，那么$\theta n$也可以描述这个旋转。从旋转向量到旋转矩阵的转换过程有罗德里格斯公式表明：

$$\boldsymbol{R}=\cos\theta\boldsymbol{I}+(1-\cos\theta)\boldsymbol{n}\boldsymbol{n}^\mathrm{T}+\sin\theta\boldsymbol{n}^\mathrm{\wedge}$$

从旋转矩阵到旋转向量：

因为

$$\begin{aligned} tr\left(R\right)& =\cos\theta\operatorname{tr}\left(\boldsymbol{I}\right)+\left(1-\cos\theta\right)\operatorname{tr}\left(\boldsymbol{n}\boldsymbol{n}^\mathrm{T}\right)+\sin\theta\operatorname{tr}(\boldsymbol{n}^{\wedge}) \\ &=3\cos\theta+(1-\cos\theta) \\ &=1+2\cos\theta \end{aligned}$$

所以

$$\theta=\arccos\frac{\operatorname{tr}(\boldsymbol{R})-1}2$$

关于转轴$n$，旋转轴上的向量在旋转后不发生改变，说明：

$$Rn=n$$

因此，转轴$n$是矩阵$R$特征值1对应的特征向量。

2.欧拉角

欧拉角使用了3个分离的转角，把一个旋转分解成3次不同轴的旋转。一般情况下，我们使用”偏航-俯仰-滚转“（yaw-pitch-roll）3个角度来描述一个旋转。它等价于ZYX轴的旋转：

• 绕物体的Z轴旋转，得到偏航角yaw。
• 绕旋转之后的Y轴旋转，得到俯仰角pitch。
• 绕旋转之后的X轴旋转，得到滚转角。

四元数

1.定义

在二维情况下，旋转可以由单位复数来描述。类似地，我们用四元数描述三维旋转：

一个四元数$q$拥有一个实部和三个虚部：

$$\mathbf{q}=q_0+q_1\mathbf{i}+\mathbf{q}_2\mathbf{j}+\mathbf{q}_3\mathbf{k}$$

其中，$i,h,k$为四元数的三个虚部。满足：

$$\begin{cases}\mathrm{i^2=j^2=k^2=-1}\\[2ex]\mathrm{ij=k,ji=-k}\\[2ex]\mathrm{jk=i,kj=-i}\\[2ex]\mathrm{ki=j,ik=-j}\end{cases}$$

2.转换成旋转矩阵

用四元数表示旋转

把三维空间点$p$用一个虚四元数来描述：

$$\boldsymbol{p}=[0,x,y,z]^\mathrm{T}=[0,\boldsymbol{v}]^\mathrm{T}$$

则旋转后的$p^{\prime}$可表示为：

$$p^{\prime}=qpq^{-1}$$

我们换另一种写法，先定义如下的符号$\boldsymbol{q}^+$和$\boldsymbol{q}^\mathrm{\oplus}$

$$\boldsymbol{q}^+=\begin{bmatrix}s&-\boldsymbol{v}^\mathrm{T}\\\\\boldsymbol{v}&s\boldsymbol{I}+\boldsymbol{v}^\mathrm{\wedge}\end{bmatrix},\quad\boldsymbol{q}^\mathrm{\oplus}=\begin{bmatrix}s&-\boldsymbol{v}^\mathrm{T}\\\\\boldsymbol{v}&s\boldsymbol{I}-\boldsymbol{v}^\mathrm{\wedge}\end{bmatrix}$$

有：

$$q_1^+q_2=\begin{bmatrix}s_1&-\boldsymbol{v}_1^\mathrm{T}\\\\v_1&s_1\boldsymbol{I}+\boldsymbol{v}_1^\mathrm{\wedge}\end{bmatrix}\begin{bmatrix}s_2\\\\v_2\end{bmatrix}=\begin{bmatrix}-\boldsymbol{v}_1^\mathrm{T}\boldsymbol{v}_2+s_1s_2\\\\s_1\boldsymbol{v}_2+s_2\boldsymbol{v}_1+\boldsymbol{v}_1^\mathrm{\wedge}\boldsymbol{v}_2\end{bmatrix}=\boldsymbol{q}_1\boldsymbol{q}_2$$

则：

$$\begin{aligned}p^{\prime}&=qpq^{-1}\\&=q^{+}p^{+}q^{-1}\\&=q^{+}q^{-1\oplus}p\end{aligned}$$ $$\begin{align} \boldsymbol{q}^+\left(\boldsymbol{q}^{-1}\right)^\oplus & = \begin{bmatrix}s&-\boldsymbol{v}^\mathrm{T}\\\\\boldsymbol{v}&s\boldsymbol{I}+\boldsymbol{v}^\mathrm{\wedge}\end{bmatrix}\begin{bmatrix}s&\boldsymbol{v}^\mathrm{T}\\\\-\boldsymbol{v}&s\boldsymbol{I}+\boldsymbol{v}^\mathrm{\wedge}\end{bmatrix}\\ & = \begin{bmatrix}1&\boldsymbol{0}\\\boldsymbol{0}^\mathrm{T}&\boldsymbol{v}\boldsymbol{v}^\mathrm{T}+s^2\boldsymbol{I}+2s\boldsymbol{v}^\mathrm{\wedge}+\left(\boldsymbol{v}^\mathrm{\wedge}\right)^2\end{bmatrix} \end{align}$$

得：

$$R=vv^{\mathrm{T}}+s^2I+2s\boldsymbol{v}^{\wedge}+\left(\boldsymbol{v}^{\wedge}\right)^2 \tag{1}$$

3.转换成旋转向量

对式(1)两侧求迹，得

$$\begin{aligned} \text{tr(R)}& =\operatorname{tr}(\boldsymbol{v}\boldsymbol{v}^\mathrm{T}+3s^2+2s\cdot0+\operatorname{tr}((\boldsymbol{v}^\wedge)^2) \\ &=v_1^2+v_2^2+v_3^2+3s^2-2(v_1^2+v_2^2+v_3^2) \\ &=(1-s^2)+3s^2-2(1-s^2) \\ &=4s^2-1 \end{aligned}$$

由旋转向量和旋转矩阵之间得转换公式得

$$\begin{aligned}\theta&=\arccos\frac{\mathrm{tr}(\boldsymbol{R}-1)}{2}\\&=\arccos(2s^2-1).\end{aligned}$$

即

$$\cos\theta=2s^2-1=2\cos^2\frac{\theta}{2}-1$$

所以

$$\theta=2\arccos s$$

总之，四元数到旋转向量的转换公式如下：

$$\left\{\begin{array}{l} \theta=2 \arccos q_{0} \\ {\left[n_{x}, n_{y}, n_{z}\right]^{\mathrm{T}}=\left[q_{1}, q_{2}, q_{3}\right]^{\mathrm{T}} / \sin \frac{\theta}{2}} \end{array}\right.$$

李群李代数

群

$$\begin{aligned} &\text{SO(3)} =\{\boldsymbol{R}\in\mathbb{R}^{3\times3}|\boldsymbol{RR}^{\mathrm{T}}=\boldsymbol{I},\det(\boldsymbol{R})=1\}, \\ &\text{SE(3)} =\left\{\boldsymbol{T}=\begin{bmatrix}\boldsymbol{R}&\boldsymbol{t}\\\\\boldsymbol{0}^\mathrm{T}&1\end{bmatrix}\in\mathbb{R}^{4\times4}|\boldsymbol{R}\in\mathrm{SO}(3),\boldsymbol{t}\in\mathbb{R}^3\right\} \end{aligned}$$

上式分别为三维旋转矩阵集合和三维变换矩阵集合，分别构成了特殊正交群SO(3)和特殊欧式群SE(3)。

群是一种集合加上一种运算的代数结构。我们把集合记作$A$，运算记作$\cdot $，那么群可以记作$G=(A,\cdot)$。群要求这个运算满足以下几个条件：

1. 封闭性：$\forall a_1,a_2\in A,\quad a_1\cdot a_2\in A$
2. 结合律：$\forall a_1,a_2,a_3\in A,\quad(a_1\cdot a_2)\cdot a_3=a_1\cdot(a_2\cdot a_3)$
3. 幺元：$\exists a_0\in A,\quad\mathrm{s.t.}\quad\forall a\in A,\quad a_0\cdot a=a\cdot a_0=a$
4. 逆：$\forall a\in A,\quad\exists a^{-1}\in A,\quad\text{s.t.}\quad a\cdot a^{-1}=a_0$

李群是指具有连续光滑性质的群。

李代数

李代数描述了李群的局部性质。准确的讲是单位元附近的正切空间。

李代数由一个集合$V$、一个数域$F$和一个二元运算$[,]$组成。如果满足以下几条性质，则称$(\mathbb{V},\mathbb{F},[,])$为一个李代数，记作$\mathfrak{g}$。

1. 封闭性：$\forall X,\boldsymbol{Y}\in\mathbb{V},[\boldsymbol{X},\boldsymbol{Y}]\in\mathbb{V}$

2. 双线性：$\forall X,Y,Z\in\mathbb{V},a,b\in\mathbb{F}$，有

   $$[a\boldsymbol{X}+b\boldsymbol{Y},\boldsymbol{Z}]=a[\boldsymbol{X},\boldsymbol{Z}]+b[\boldsymbol{Y},\boldsymbol{Z}],\quad[\boldsymbol{Z},a\boldsymbol{X}+b\boldsymbol{Y}]=a[\boldsymbol{Z},\boldsymbol{X}]+b[\boldsymbol{Z},\boldsymbol{Y}]$$

3. 自反性：$\forall X\in\mathbb{V},[X,X]=\mathbf{0}$

4. 雅可比等价：$\forall X,Y,Z\in\mathbb{V},[X,[Y,Z]]+[Z,[X,Y]]+[Y,[Z,X]]=\mathbf{0}$

李代数$\mathfrak{so}(3)$

$SO(3)$对应的李代数是定义在$\mathbb{R}^3$上的向量，我们记作$\phi$，其反对称矩阵为：

$$\boldsymbol{\Phi}=\boldsymbol{\phi}^\wedge=\begin{bmatrix}0&-\phi_3&\phi_2\\\\\phi_3&0&-\phi_1\\\\-\phi_2&\phi_1&0\end{bmatrix}\in\mathbb{R}^{3\times3}$$

此定义下，李括号为：

$$[\phi_1,\phi_2]=(\boldsymbol{\Phi}_1\boldsymbol{\Phi}_2-\boldsymbol{\Phi}_2\boldsymbol{\Phi}_1)^\vee$$

则$\mathfrak{so}(3)$为：

$$\mathfrak{so}(3)=\left\{\phi\in\mathbb{R}^3,\boldsymbol{\Phi}=\boldsymbol{\phi}^\wedge\in\mathbb{R}^{3\times3}\right\}$$

三维旋转矩阵$R$（李群）与l李代数$\mathfrak{so}(3)$的关系由指数映射恒定：

$$R=\exp(\phi^{\wedge})$$

李代数$\mathfrak{se}(3)$

与旋转矩阵类似地，对于$SE(3)$也有对应的李代数$\mathfrak{se}(3)$。其定义为：

$$\mathfrak{sc}(3)=\left\{\boldsymbol{\xi}=\begin{bmatrix}\rho\\\phi\end{bmatrix}\in\mathbb{R}^6,\boldsymbol{\rho}\in\mathbb{R}^3,\boldsymbol{\phi}\in\mathfrak{so}(3),\boldsymbol{\xi}^\wedge=\begin{bmatrix}\boldsymbol{\phi}^\wedge&\boldsymbol{\rho}\\\\\boldsymbol{0}^\mathrm{T}&0\end{bmatrix}\in\mathbb{R}^{4\times4}\right\}$$

我们把每个$\mathfrak{se}(3)$元素记作$\xi$，它是一个六维向量。前三维为平移（但含义与变换矩阵中的平移不同），记作$\rho$；后三维为旋转，记作$\phi$，实质上是元素$\mathfrak{so}(3)$。同时，我们拓展了^符号的含义。在$\mathfrak{se}(3)$中，同样使用＾符号，将一个六维向量转换成四维矩阵，但这里不再表示反对称：

$$\boldsymbol{\xi}^\wedge=\begin{bmatrix}\boldsymbol{\phi}^\wedge&\boldsymbol{\rho}\\\boldsymbol{0}^\mathrm{T}&0\end{bmatrix}\in\mathbb{R}^{4\times4}$$

李括号定义为：

$$[\boldsymbol{\xi}_1,\boldsymbol{\xi}_2]=(\boldsymbol{\xi}_1^\wedge\boldsymbol{\xi}_2^\wedge-\boldsymbol{\xi}_2^\wedge\boldsymbol{\xi}_1^\wedge)^\vee$$

指数映射与对数映射

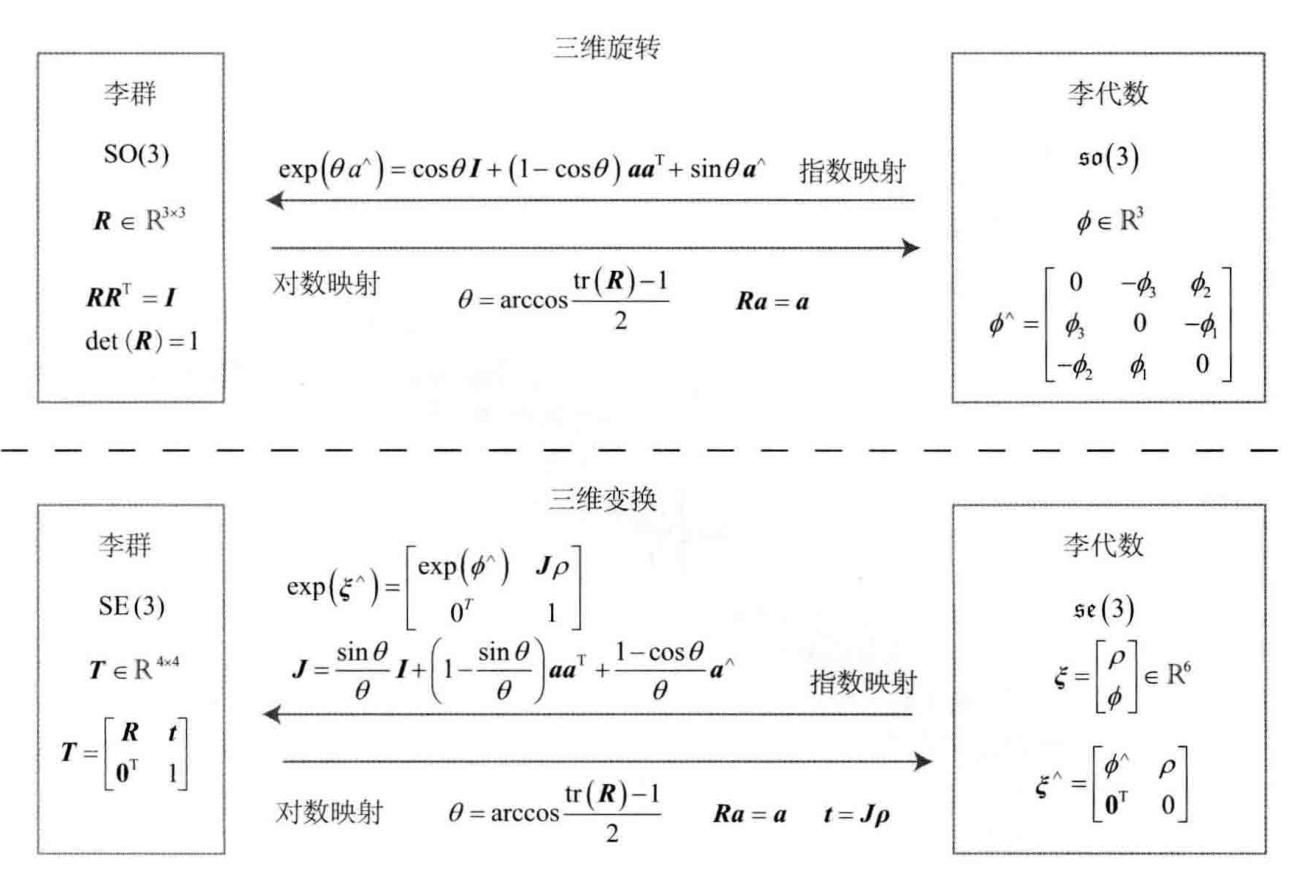
其中，由于$\phi$是三维向量，我们可以定义它的模长和方向，分别记作$\theta$和$a$

$$\phi=\theta\boldsymbol{a}$$

BCH公式与近似形式

$$\ln\left(\exp\left(\phi_1^{\wedge}\right)\exp\left(\phi_2^{\wedge}\right)\right)^{\vee}\approx\begin{cases}J_l\left(\phi_2\right)^{-1}\phi_1+\phi_2&\text{当}\phi_1\text{为小量},\\J_r\left(\phi_1\right)^{-1}\phi_2+\phi_1&\text{当}\phi_2\text{为小量}.\end{cases}$$

以第一个近似为例。该式告诉我们，当对一个旋转矩阵$R2$（李代数为$\phi_2$）左乘一个微小旋转矩阵$R1$（李代数为$\phi_1$）时，可以近似地看作，在原有的李代数$\phi_2$上加上了一项$\boldsymbol{J}_l(\boldsymbol{\phi}_2)^{-1}\boldsymbol{\phi}_1$。同理，第二个近似描述了右乘一个微小位移的情况。于是，李代数在BCH近似下，分成了左乘近似和右乘近似两种，在使用时我们须注意使用的是左乘模型还是右乘模型。

以左乘为例：

$$\boldsymbol{J}_l=\boldsymbol{J}=\frac{\sin\theta}\theta\boldsymbol{I}+\left(1-\frac{\sin\theta}\theta\right)\boldsymbol{a}\boldsymbol{a}^\mathrm{T}+\frac{1-\cos\theta}\theta\boldsymbol{a}^\wedge$$

它的逆为：

$$J_r(\phi)=\boldsymbol{J}_l(-\boldsymbol{\phi})$$

所以在$SO(3)$中，有

$$\exp\left(\Delta\phi^{\wedge}\right)\exp\left(\phi^{\wedge}\right)=\exp\left(\left(\phi+J_{l}^{-1}\left(\phi\right)\Delta\phi\right)^{\wedge}\right)$$ $$\exp\left((\phi+\Delta\phi)^{\uparrow}\right)=\exp\left((J_l\Delta\phi)^{\uparrow}\right)\exp\left(\phi^{\uparrow}\right)=\exp\left(\phi^{\uparrow}\right)\exp\left((J_r\Delta\phi)^{\uparrow}\right)$$

同样的在$SE(3)$中，有

$$\begin{aligned}\exp\left(\Delta\boldsymbol{\xi}^\wedge\right)\exp\left(\boldsymbol{\xi}^\wedge\right)&\approx\exp\left(\left(\boldsymbol{J}_l^{-1}\Delta\boldsymbol{\xi}+\boldsymbol{\xi}\right)^\wedge\right)\\\exp\left(\boldsymbol{\xi}^\wedge\right)\exp\left(\Delta\boldsymbol{\xi}^\wedge\right)&\approx\exp\left(\left(\boldsymbol{J}_r^{-1}\Delta\boldsymbol{\xi}+\boldsymbol{\xi}\right)^\wedge\right)\end{aligned}$$

李代数求导

SO(3)上的李代数求导：

$$\begin{aligned} \frac{\partial\left(\exp \left(\boldsymbol{\phi}^{\wedge}\right) \boldsymbol{p}\right)}{\partial \boldsymbol{\phi}} & =\lim _{\delta \boldsymbol{\phi} \rightarrow \mathbf{0}} \frac{\exp \left((\boldsymbol{\phi}+\delta \boldsymbol{\phi})^{\wedge}\right) \boldsymbol{p}-\exp \left(\boldsymbol{\phi}^{\wedge}\right) \boldsymbol{p}}{\delta \boldsymbol{\phi}} \\ & =\lim _{\delta \boldsymbol{\phi} \rightarrow \mathbf{0}} \frac{\exp \left(\left(\boldsymbol{J}_{l} \delta \boldsymbol{\phi}\right)^{\wedge}\right) \exp \left(\boldsymbol{\phi}^{\wedge}\right) \boldsymbol{p}-\exp \left(\boldsymbol{\phi}^{\wedge}\right) \boldsymbol{p}}{\delta \boldsymbol{\phi}} \\ & =\lim _{\delta \boldsymbol{\phi} \rightarrow \mathbf{0}} \frac{\left(\boldsymbol{I}+\left(\boldsymbol{J}_{l} \delta \boldsymbol{\phi}\right)^{\wedge}\right) \exp \left(\boldsymbol{\phi}^{\wedge}\right) \boldsymbol{p}-\exp \left(\boldsymbol{\phi}^{\wedge}\right) \boldsymbol{p}}{\delta \boldsymbol{\phi}} \\ & =\lim _{\delta \boldsymbol{\phi} \rightarrow \mathbf{0}} \frac{\left(\boldsymbol{J}_{l} \delta \boldsymbol{\phi}\right)^{\wedge} \exp \left(\boldsymbol{\phi}^{\wedge}\right) \boldsymbol{p}}{\delta \boldsymbol{\phi}} \\ & =\lim _{\delta \boldsymbol{\phi} \rightarrow \mathbf{0}} \frac{-\left(\exp \left(\boldsymbol{\phi}^{\wedge}\right) \boldsymbol{p}\right)^{\wedge} \boldsymbol{J}_{l} \delta \boldsymbol{\phi}}{\delta \boldsymbol{\phi}} \\ & =-(\boldsymbol{R} \boldsymbol{p})^{\wedge} \boldsymbol{J}_{l} \end{aligned}$$

扰动模型（左乘）：

$$\begin{aligned} \frac{\partial(\boldsymbol{R} \boldsymbol{p})}{\partial \boldsymbol{\varphi}} & =\lim _{\boldsymbol{\varphi} \rightarrow 0} \frac{\exp \left(\boldsymbol{\varphi}^{\wedge}\right) \exp \left(\phi^{\wedge}\right) \boldsymbol{p}-\exp \left(\boldsymbol{\phi}^{\wedge}\right) \boldsymbol{p}}{\boldsymbol{\varphi}} \\ & =\lim _{\boldsymbol{\varphi} \rightarrow 0} \frac{\left(\boldsymbol{I}+\boldsymbol{\varphi}^{\wedge}\right) \exp \left(\phi^{\wedge}\right) \boldsymbol{p}-\exp \left(\boldsymbol{\phi}^{\wedge}\right) \boldsymbol{p}}{\boldsymbol{\varphi}} \\ & =\lim _{\boldsymbol{\varphi} \rightarrow 0} \frac{\boldsymbol{\varphi}^{\wedge} \boldsymbol{R} \boldsymbol{p}}{\varphi}=\lim _{\boldsymbol{\varphi} \rightarrow 0} \frac{-(\boldsymbol{R} \boldsymbol{p})^{\wedge} \boldsymbol{\varphi}}{\boldsymbol{\varphi}} \\ & =-(\boldsymbol{R} \boldsymbol{p})^{\wedge} \end{aligned}$$

SE(3)上的李代数求导

$$\begin{align} \frac{\partial\left(\boldsymbol{Tp}\right)}{\partial\delta\boldsymbol{\xi}} &=\lim_{\delta\boldsymbol{\xi}\to\boldsymbol{0}}\frac{\exp\left(\delta\boldsymbol{\xi}^{\wedge}\right)\exp\left(\boldsymbol{\xi}^{\wedge}\right)\boldsymbol{p}-\exp\left(\boldsymbol{\xi}^{\wedge}\right)\boldsymbol{p}}{\delta\boldsymbol{\xi}} \\ &=\lim_{\delta\boldsymbol{\xi}\to\mathbf{0}}\frac{\left(\boldsymbol{I}+\delta\boldsymbol{\xi}^{\wedge}\right)\exp\left(\boldsymbol{\xi}^{\wedge}\right)\boldsymbol{p}-\exp\left(\boldsymbol{\xi}^{\wedge}\right)\boldsymbol{p}}{\delta\boldsymbol{\xi}} \\ &=\lim_{\delta\boldsymbol{\xi}\to\mathbf{0}}\frac{\delta\boldsymbol{\xi}^\wedge\exp\left(\boldsymbol{\xi}^\wedge\right)\boldsymbol{p}}{\delta\boldsymbol{\xi}} \\ &=\lim_{\delta\boldsymbol{\xi}\to\mathbf{0}}\frac{\begin{bmatrix}\delta\boldsymbol{\phi}^\wedge&\delta\boldsymbol{\rho}\\\mathbf{0}^\mathrm{T}&0\end{bmatrix}\begin{bmatrix}\boldsymbol{Rp}+\boldsymbol{t}\\\\1\end{bmatrix}}{\delta\boldsymbol{\xi}} \\ &=\lim_{\delta\boldsymbol{\xi}\to\boldsymbol{0}}\frac{\begin{bmatrix}\delta\boldsymbol{\phi}^{\wedge}\left(\boldsymbol{R}\boldsymbol{p}+\boldsymbol{t}\right)+\delta\boldsymbol{\rho}\\\mathbf{0}^{\mathrm{T}}\end{bmatrix}}{[\delta\boldsymbol{\rho},\delta\boldsymbol{\phi}]^{\mathrm{T}}} \\ &=\begin{bmatrix}\boldsymbol{I}&-(\boldsymbol{R}\boldsymbol{p}+\boldsymbol{t})^{\wedge}\\\mathbf{0}^{\mathrm{T}}&\boldsymbol{0}^{\mathrm{T}}\end{bmatrix} \\ &\overset{\mathrm{def}}{\operatorname*{=}}(\boldsymbol{T}\boldsymbol{p})^{\odot} \end{align}$$