机器人中的数值优化（五）

文档维护：Arvin

网页部署：Arvin

▶

写在前面：本文内容是作者在深蓝学院机器人中的数值优化学习时的笔记，作者按照自己的理解进行了记录，如果有错误的地方还请执政。如涉侵权，请联系删除。

附录(笔记)

函数的光滑技巧

Inf convolution卷积

Inf convolution 卷积操作适应于凸函数，Inf convolution 卷积操作的目标是把不光滑的凸函数进行光滑近似，并使得光滑近似后的函数于原函数尽量吻合。   

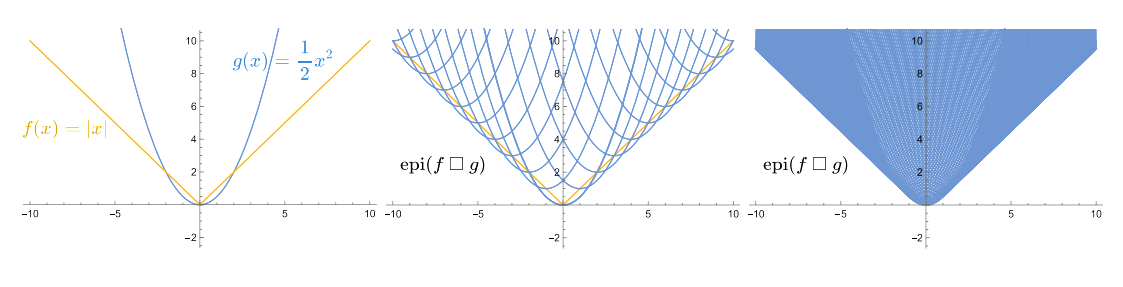
对于两个凸函数$f_1， f_2$，它们之间的Inf convolution 卷积操作记为$f_1\Box f_2$，即找一个$u_1$和$u_2$，满足$u_1+u_2=x$的条件下，使得$f_1(u_1)+f_2(u_2)$最大或最小，如下面的第一个表达式所示，由于满足$u_1+u_2=x$，因此可消去一个$u$进行简化，简化后的表达式如下面第二个式子所示：

$$\begin{aligned}(f_1\Box f_2)(x)&=\inf_{(u_1,u_2)\in\mathbb{R}^d\times\mathbb{R}^d}\{f_1(u_1)+f_2(u_2):u_1+u_2=x\}\\(f_1\Box f_2)(x)&=\inf_{u\in\mathbb{R}^d}\{f_1(u)+f_2(x-u)\}\end{aligned}$$

Inf convolution卷积具有对称性，即$f_1 \Box f_2=f_2 \Box f_1$

Inf convolution卷积操作的几何解释如下图所示，其原理就是拿光滑凸函数的轮廓去把不光滑的地方利用包络将其变成光滑的。

Moreau包络

Moreau envelope是Inf convolution卷积操作的一个特例，即将被卷积函数更改为一个二次函数或者说范数的平方，如下式所示：

$$^\gamma f:=f\Box\left(\frac1{2\gamma}\|\cdot\|^2\right)$$

其具体表达式如下式所示：

$$^\gamma f(x):=\inf_{u\in\mathbb{R}^d}\{f(u)+\frac1{2\gamma}\left\|x-u\right\|^2\}$$

当一个函数时封闭的凸函数时，inf一定可以取到最小值，$\gamma$具有平滑参数的作用，$\gamma$越小，平滑后的函数与原函数越接近。

Pinball case

Pinball loss定义为：

$$\ell_{s_1,s_2}(x)=\begin{cases}s_1x&\quad\text{if}x\le0\\s_2x&\quad\text{if}x\ge0\end{cases}$$

其中$s_1 \leq 0 \leq s_2$，Pinball函数的Moreau包络函数如下所示：

$$^\gamma f(x)=(f\Box g)(x)==\quad\begin{cases}s_1x-\gamma\frac{s_1^2}{2},&\text{if}x<s_1\\\frac{1}{2\gamma}x^2,&\text{if}x\in[\gamma s_1,\gamma s_2]\\s_2x-\gamma\frac{s_2^2}{2},&\text{if}x>s_2\end{cases}$$

一个经典的例子是Huber函数$\ell_{-1,1}$，即$s_1$取-1，$s_2$取1

当我们不断地把$\gamma$值减小，平滑后的函数与原函数也更加接近，包络的下边缘也会越来越尖，如下图所示：

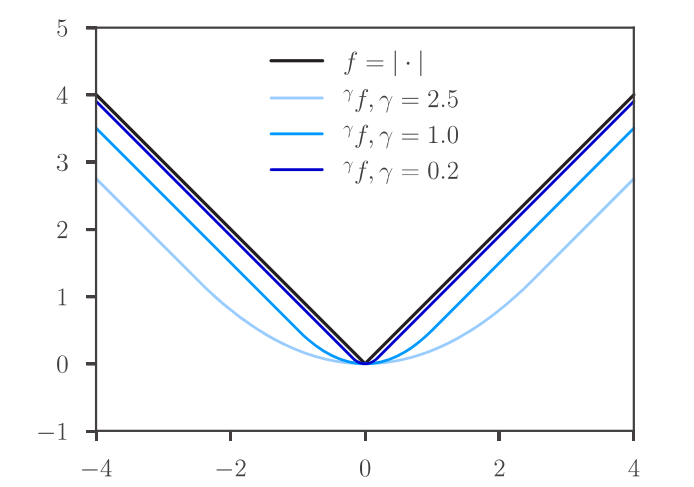
Moreau 包络具有一个良好的性质，即一个函数与它的Moreau 包络函数的最小值相同，即

$$\forall\gamma>0,\quad\inf_x\left((^\gamma f)(x)\right)=\inf_xf(x)$$

证明如下：

$$\begin{aligned} \inf_x\left((^\gamma f)(x)\right)& =\inf_x\inf_y\left\{f(y)+\frac1{2\gamma}\left\|x-y\right\|^2\right\} \\ &=\inf_y\inf_x\left\{f(y)+\frac1{2\gamma}\left\|x-y\right\|^2\right\} \\ &=\inf_yf(y) \end{aligned}$$

总结一下，用Inf convolution 卷积操作可以对一个不光滑的凸函数进行平滑，平滑后的函数与原函数具有同样的最小值，给一个光滑因子$\gamma$用来调节光滑程度，我们把不光滑的凸函数$f$的光滑近似记作${\overset{\gamma}{\omega}}f$，$\omega$是我们用来光滑$f$的被卷积的函数，$\omega$取$\frac12|\cdot|^2$时，就是Moreau 包络。

Mollifier-Conv

Mollifier卷积是比Inf-conv卷积更一般化的卷积，举一个例子，对于如式所示的函数，它是通过$e^{\frac{-1}{1-x^2}}$变化而来的，除以其自身的积分相当于进行了缩放操作，这样一个凸起的或者说隆起的函数就称为Mollifier。

$$\varphi(x)=\begin{cases}\frac{e^{-1/(1-x^2)}}{\int_{-1}^1e^{-1/(1-s^2)}\mathrm{d}s}&\mathrm{~if~}|x|<1\\0&\mathrm{~if~}|x|\geq1&\end{cases}$$

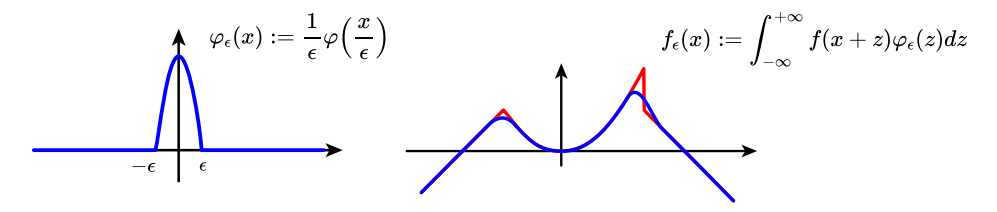
更一般的，取$\varphi_\epsilon(x):=\frac{1}{\epsilon}\varphi\Big(\frac{x}{\epsilon}\Big)$，将该函数与下面右图中红色曲线所示的函数进行卷积$f_\epsilon(x):=\int_{-\infty}^{+\infty}f(x+z)\varphi_\epsilon(z)dz$，得到了下面右图中的蓝色曲线,其中$\epsilon$用于调节光滑效果，$\epsilon$越小光滑效果越差，越接近于原函数。

下图中给出了一个二维的例子，在一维的基础上进行了推广

$$\varphi(x)=\begin{cases}\frac{e^{-1/(1-\|x\|^2)}}{\int_{\mathbb{R}^n}e^{-1/(1-\|s\|^2)}\mathrm{d}s}&\text{if}\|x\|<1\\0&\text{if}\|x\|\geq1\end{cases}$$

$$\begin{gathered}\varphi_\epsilon(x):=\frac1{\epsilon^n}\varphi{\left(\frac x\epsilon\right)}\\\\f_\epsilon(x):=\int_{-\infty}^{+\infty}f(x+z)\varphi_\epsilon(z)dz\end{gathered}$$

Mollifier的具体定义如下：

$$\begin{aligned}&\int_{\mathbb{R}^n}\varphi(x)\mathrm{d}x=1\\&\lim_{\epsilon\to0}\varphi_\epsilon(x)=\lim_{\epsilon\to0}\epsilon^{-n}\varphi(x/\epsilon)=\delta(x)\end{aligned}$$

$\varphi(x)$满足在$\mathbb{R}^n $上积分为1，且当$\epsilon$趋向于0时，$\varphi(x)$趋于冲激函数$\delta(x)$，满足这两个条件即可称为Mollifier。

为何使用Mollifier函数对原函数进行卷积操作会使其变得光滑？下面使推导：

$$\begin{aligned} \frac d{dx}f_{\epsilon}(x)& =\frac d{dx}\int f(x+z)\varphi_\epsilon(z)\mathrm{d}z \\ &=\frac d{dx}\int f(y)\varphi_\epsilon(y-x)dy \\ &=\int f(y)\biggl(\frac d{dx}\varphi_{\epsilon}(y-x)\biggr)dy \end{aligned}$$

若Mollifier函数是处处连续可微的，则对某个函数进行卷积操作后得到的函数也是处处连续的。

举个例子

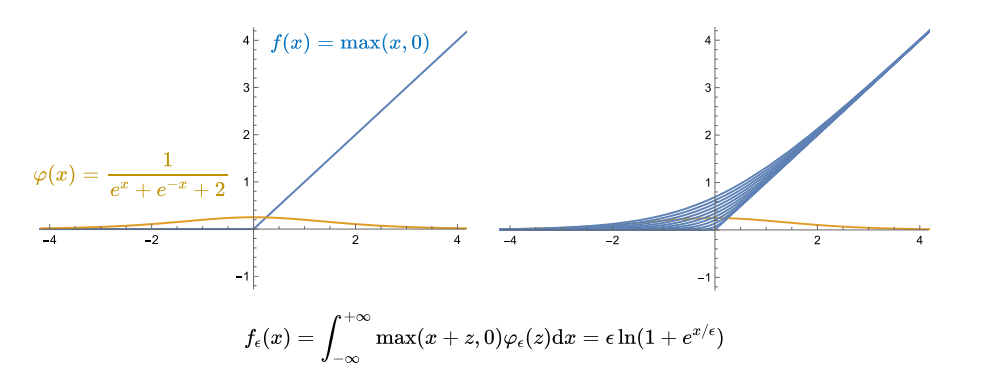
伴随灵敏度分析

伴随灵敏度分析可以避免冗余信息的计算，在下面的例子中，我们想要求解$Ax=b1、Ax=b2 … Ax=bm$等一系列方程组，第一种求解思路是将$A$矩阵进行LU分解，$A = L U$ ，求逆后可得到 $A^{-1}= U^{-1}L^{-1}$ ，然后依次将$b1\sim bm$代入下式即可得到这一系列方程组的解。

$$x_i=U^{-1}L^{-1}b_i$$

但如果我们事先知道需要使用那些数据，那么我们能不能仅把需要使用的变量求出来？比如我们的目标是求每个$x_i$的平均值$a_i$，比如所有$x_1$的平均值$a_1$，那么我们是不是不需要求出每个$X_i$的具体值，而仅仅需要他们的平均值$a_i$。

$$a_i=c^Tx_i=c^TA^{-1}b_i=b_i^TA^{-T}c$$

之前需要先算$A^{-1}b_i$部分，再算$c^TA^{-1}b_i$，现在可以先算$c^TA^{-1}b_i$，再算$A^{-T}c$，我们不需要对每个$b_i$求一个线性方程组了，仅需要求一个方程组$q\equiv A^{-T}c$，求出$q$之后，再与$b_i$做一个点积即可，$a_i=b_{i}^{T}q$。

伴随灵敏度分析的思想是在计算矩阵相乘的时候考虑那个先乘，那个后乘。线性方程组有一个伴随线性方程组，伴随灵敏度分析允许优化一小部分设计参数，而不是全部参数。

假设X是一个线性方程组的解，它的维度很大，它是一个完备的参数，从$X$可以获得所有我们想要的信息，但我们不能直接处理这么大维度的优化，我们需要设一组设计参数$\mathbf{p}=(p_1,p_2,…,p_M)$，我们要算的是一些目标函数$g(\mathbf{p},\mathbf{x})$关于参数$p_1,p_2,\ldots,p_M$的梯度。

$$\begin{aligned}&\frac{dg}{dp_j}=\frac{\partial g}{\partial p_j}+\sum_{i=1}^N\frac{\partial g}{\partial x_i}\frac{\partial x_i}{\partial p_j}\\\\&\frac{dg}{d\mathbf{p}}=g_{\mathbf{p}}+g_{\mathbf{x}}\mathbf{x_p}\end{aligned}$$

一般来讲$\frac{\partial g}{\partial p_j}$和$\frac{\partial g}{\partial X_j}$是容易获得的，$\frac{\partial X_i}{\partial p_j}$是不知道的。

$$A_{p_j}\mathbf{x}+A\mathbf{x}_{p_j}=b_{p_j}\quad\Rightarrow\quad\mathbf{x}_{p_j}=A^{-1}[b_{p_j}-A_{p_j}\mathbf{x}]$$

我们使用矩阵相乘交换顺序的思想，把解$m$次$N^2$复杂度的方程组，转换为解一次就可以了。

线性方程组求解器的分类和特点

线性方程组求解器可分为两大类或三小类，两大类即直接求解和迭代求解，直接求解可以得到$Ax=b$的精确解，迭代求解随着迭代次数的增多，所得到的近似解与精确解的误差也逐渐减小。三小类是因为有的求解器会利用矩阵的稀疏结构，而有的求解器不利用，因此，直接法又分为稠密法和稀疏直接法。

1. 稠密法

   具有简单数据结构，不需要索引数据结构等特殊的数据结构，采用矩阵的直接表示，主要是$O(N3)$分解算法

2. 稀疏直接法

   当矩阵中有很多0元素时，我们可以仅储存非0元素的位置和具体的值，使其占较少的内存。因子分解成本取决于问题结构（1D低成本；2D可接受成本；3D高成本；不容易给出一般规则，$NP-Hard$以排序以获得最佳稀疏性）

3. 迭代法

   迭代求取近似解，仅需要知道$y=Ax\text{ (maybe }y=A^Tx)$，良好的收敛性取决于预条件。

作业

作业一：凸多面体障碍物下的路径平滑

1. 设置凸多面体

凸多面体由多个半平面组成，在三维空间里可以表示为

$$a_ix+b_iy+c_iz+d_i \le 0$$

可以将其参数化保存到.config文件里。

1. 求最短距离

求解点到凸多面体的最短距离，可以转换成SDQP

$$\begin{aligned}\min_{X\in\mathbb{R}^n}\frac{1}{2}X^\mathrm{T}M_{\mathcal{Q}}X+c_{\mathcal{Q}}^\mathrm{T}X \\ \text{s.t. }A_{\mathcal{Q}}X\le b_{\mathcal{Q}}\end{aligned}$$

求解可以用课程中提供的求解器：GitHub - ZJU-FAST-Lab/SDQP: Small-Dimensional Quadratic Programming in Linear Time

下面是转换过程：

令$X=X_r - X_o$，其中$X$是曲线插值点，即智能体问题。$X_o$是凸多面体上离$X_r$最近的点。

$X_o$是凸多面体上的点，则约束为（这里只是半平面的表示方法是根据代码框架中代码确定的$b_Q$符号）：

$$A_{Q}X_{o}+b_Q\le0$$

另$M_Q=2I$，$c_Q^{T}=0$。

则

$$\begin{aligned} &\min_{X\in\mathbb{R}^n}X^\mathrm{T}X \\ &\text{s.t. }A_{\mathcal{Q}}(X_r-X)+b_Q\le0\end{aligned}$$

则

$$\begin{aligned} &\min_{X\in\mathbb{R}^n}X^\mathrm{T}X \\ &\text{s.t. }-A_{\mathcal{Q}}X\le-(A_{\mathcal{Q}}+b_{\mathcal{Q}})\end{aligned}$$

令$A_{new} = -A_{\mathcal{Q}}$、$b_{new}=-(A_{\mathcal{Q}} + b_{\mathcal{Q}})$

$$\begin{aligned} &\min_{X\in\mathbb{R}^n}X^\mathrm{T}X \\ &\text{s.t. }A_{new}X\le b_{new}\end{aligned}$$

即可利用求解器求解出来。

1. 构造势能函数

根据人工势场函数：

$$U_{rep}(q)=\begin{cases}\frac{1}{2}\eta\bigg(\frac{1}{D(q)}-\frac{1}{Q^*}\bigg)^2,&D(q)\le Q^*\\\\0,&D(q)>Q^*\end{cases}$$

其中，${D(q)}$是距离最近障碍物的距离；$\eta$是斥力增益常量；$Q^*$是障碍物的作用阈值范围，在该阈值范围之内，障碍物才会产生斥力，超出此范围则不产生斥力影响

稍加修改：

$$Potential(x)=\begin{cases}P\bigg(\frac{1}{D+1}-\frac{1}{Q^*+1}\bigg)^2,&D\le Q^*\\\\0,&D>Q^*\end{cases}$$

其中根据求解器可以求出最短距离

$$D=\left \| X \right \| _2=\left \| X_{r}-X_{o} \right \| _2$$

可以求出梯度

$$\nabla Potential(x)=\begin{cases}2P\bigg(\frac{1}{Q^*+1}-\frac{1}{D+1}\bigg)\bigg(\frac{1}{D+1}\bigg)^2\frac{X-X_o}{\left \| X-X_o \right \|_2 +0.01 } ,&D\le Q^*\\\\0,&D>Q^*\end{cases}$$

能量函数根据之前的即可。

结果：

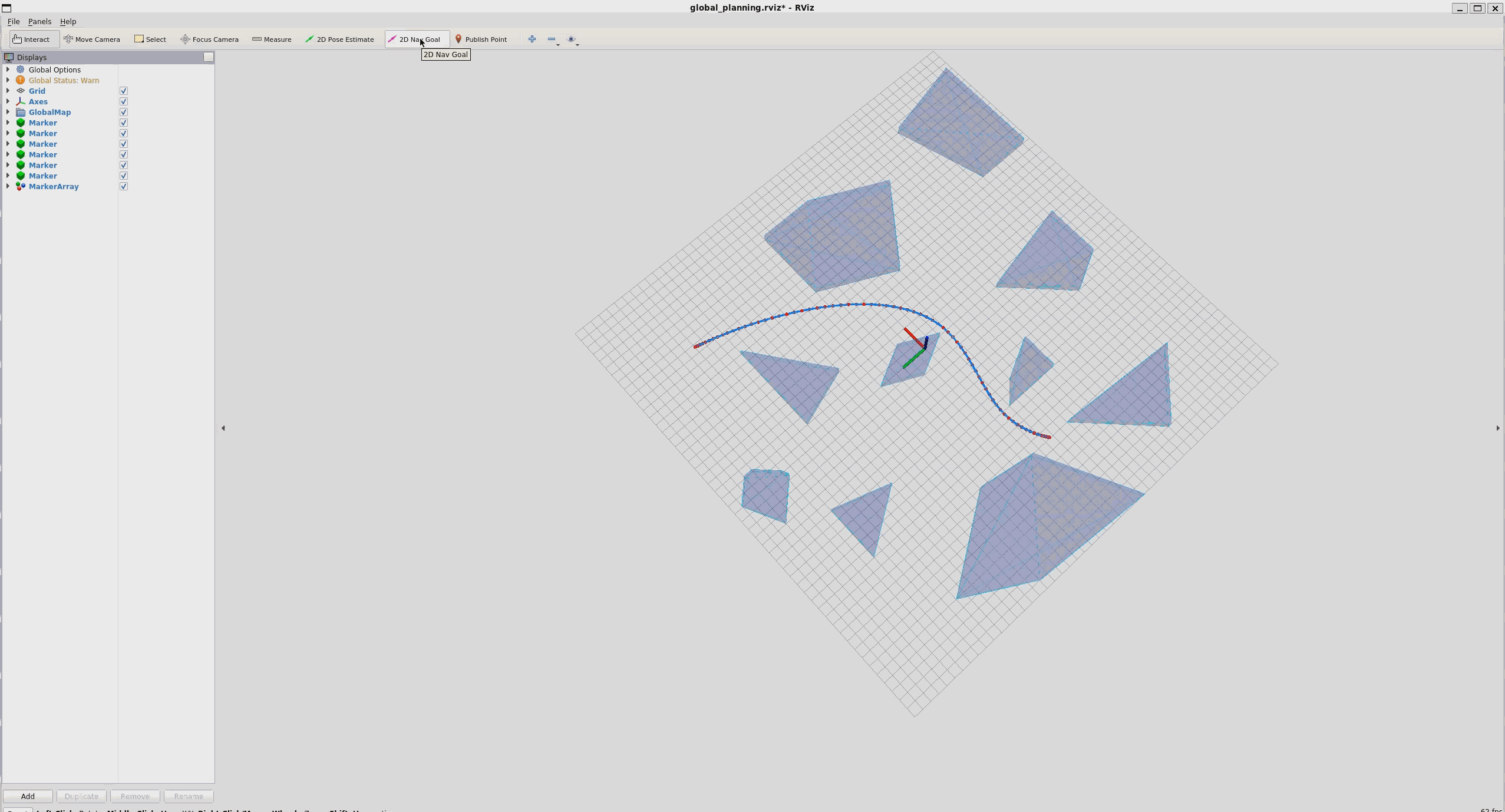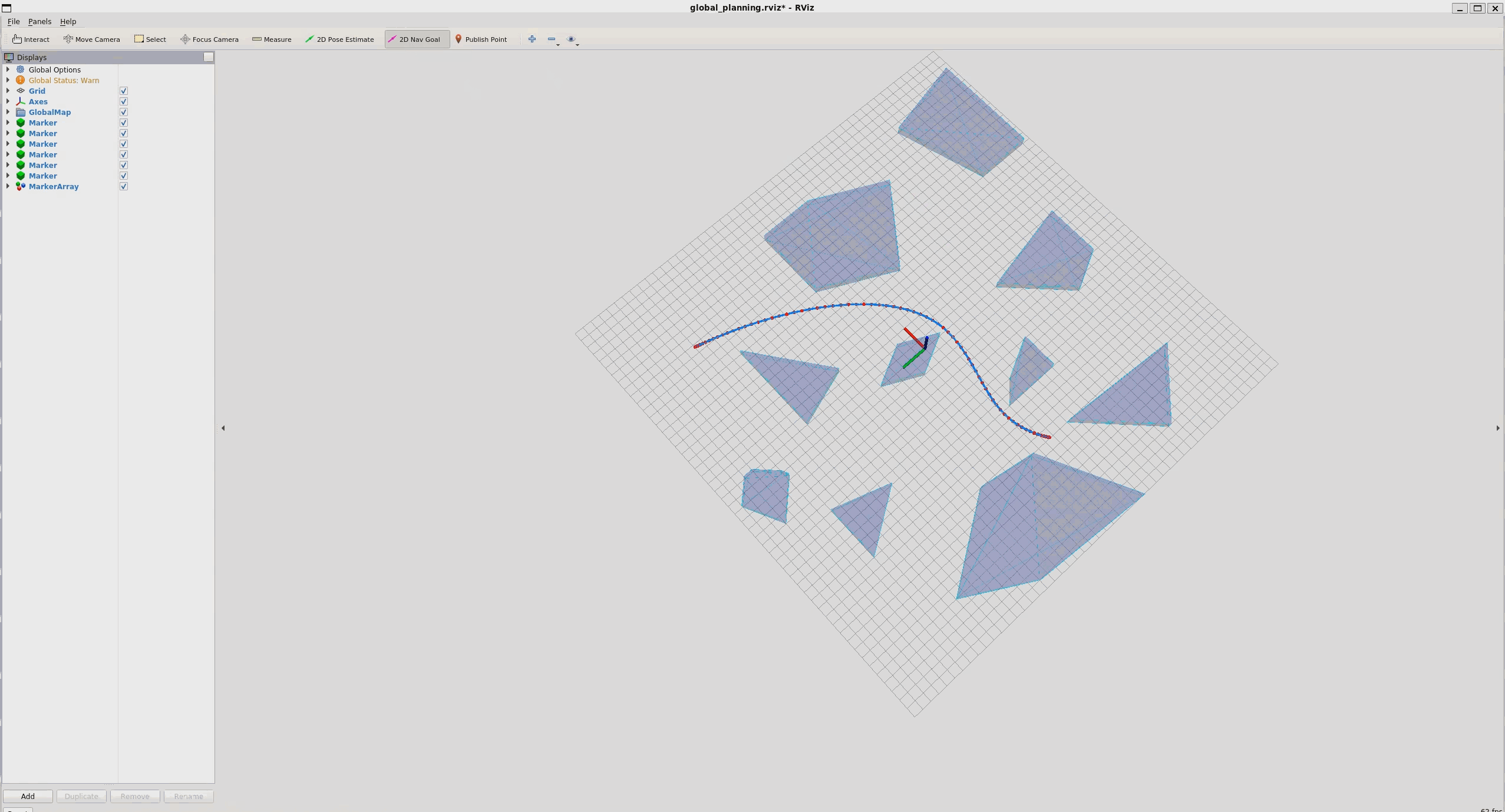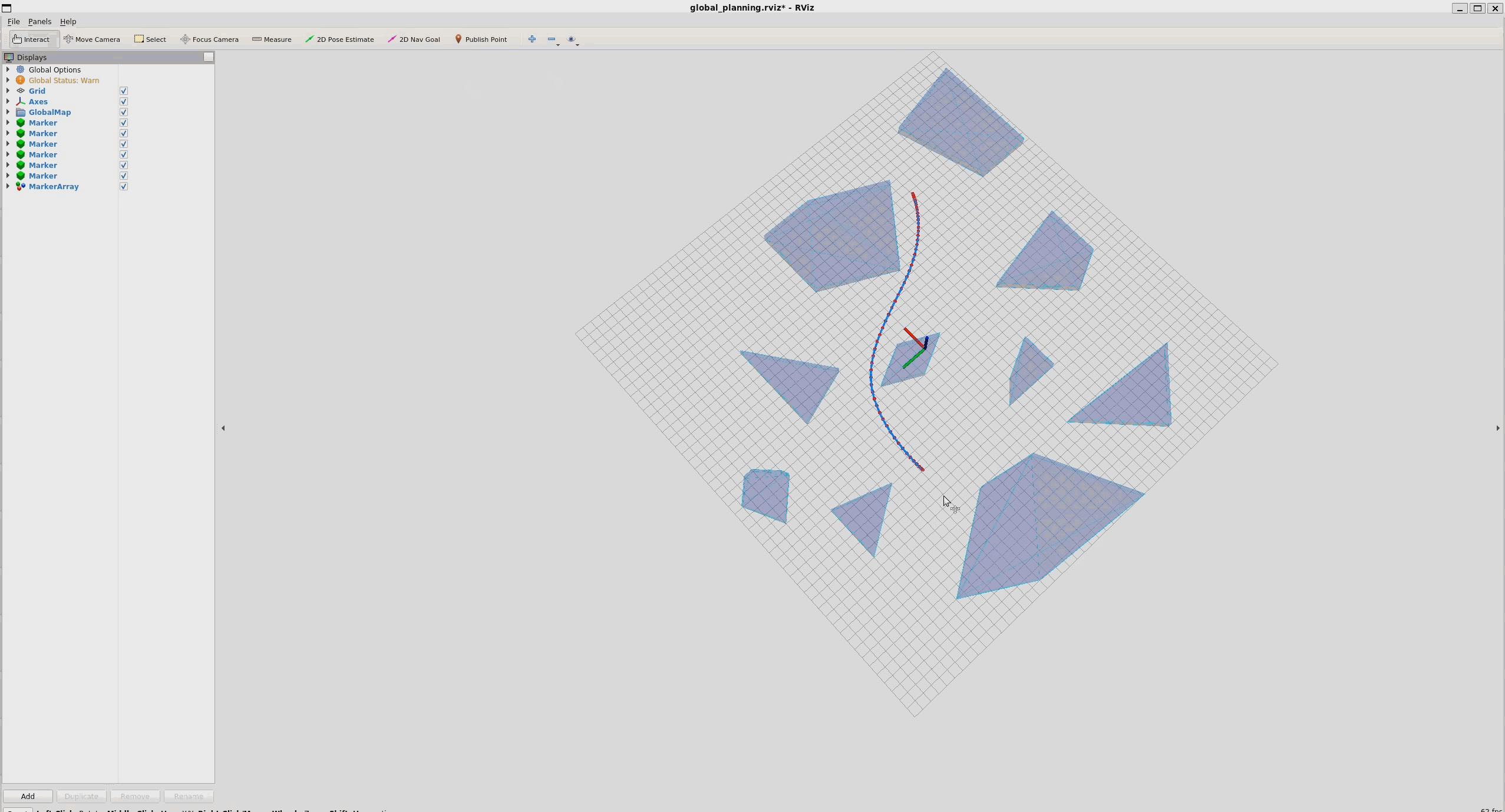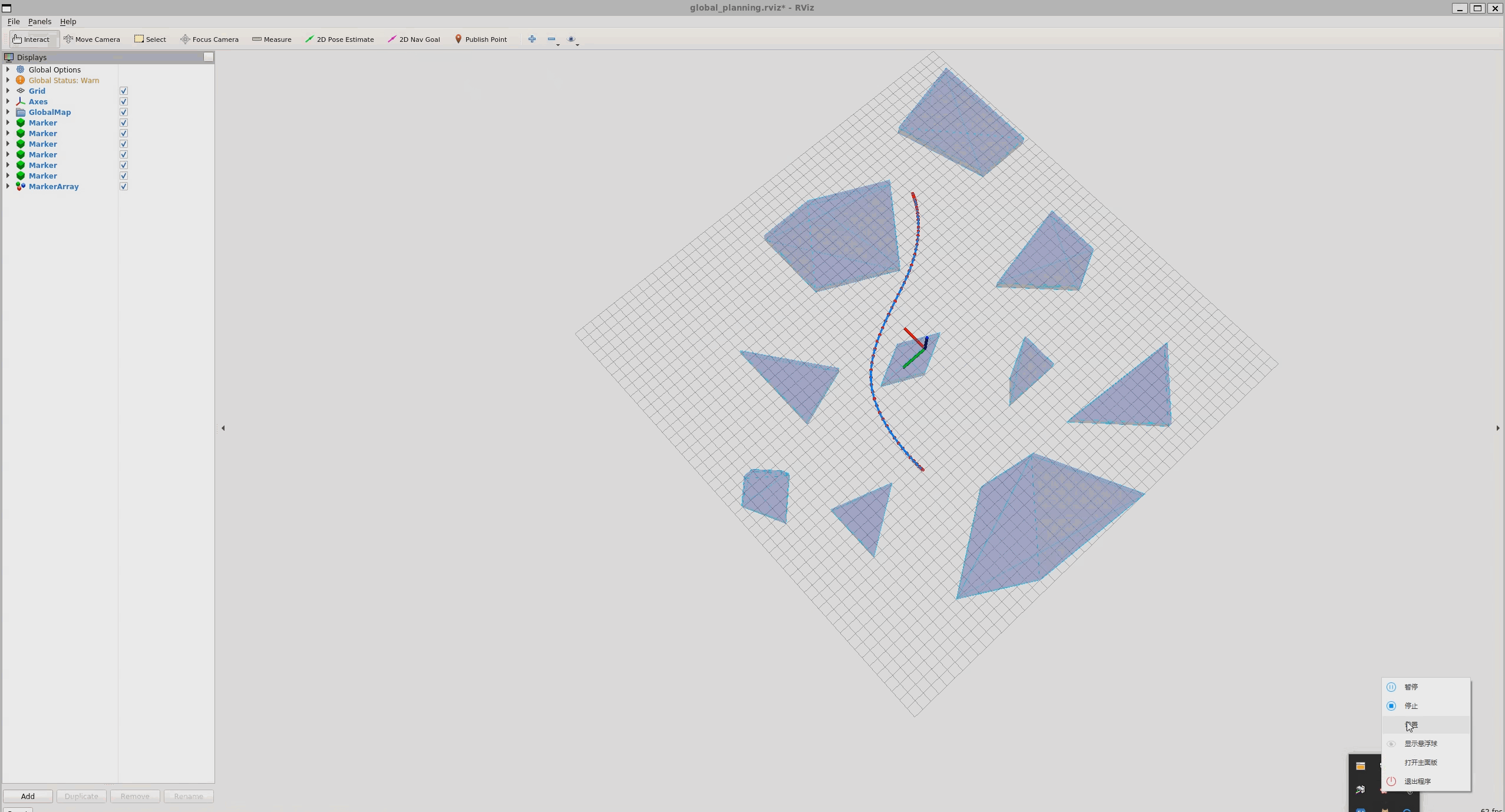
运行：

cd catkin_ws
catkin_make
source ./devel/set.bash
roslaunch gcopter curve_gen.launch