机器人中的数值优化（四）

文档维护：Arvin

网页部署：Arvin

▶

写在前面：本文内容是作者在深蓝学院机器人中的数值优化学习时的笔记，作者按照自己的理解进行了记录，如果有错误的地方还请执政。如涉侵权，请联系删除。

锥规划（笔记）

锥和对称锥

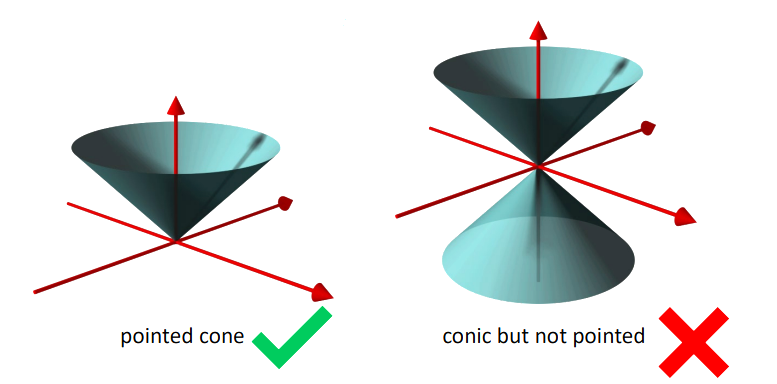
尖锥

如果一组点$\kappa\subseteq\mathbb{R}^n$满足以下条件，则称为尖锥：

$$\begin{aligned}&{\text{Conic:}\quad a\in\mathcal{K},\lambda\geq0\Rightarrow\lambda a\in\mathcal{K}}\\&{\text{Pointed:}\quad a\in\mathcal{K}\mathrm{~and~}-a\in\mathcal{K}\Rightarrow a=0}\end{aligned}$$

第一个条件即向量$a$在集合$\mathcal{K}$中，$\lambda\geq0$，则$\lambda a$也必然在集合$\mathcal{K}$中；第二个条件是若向量$a$在集合$\mathcal{K}$中，则向量$-a$不在集合$\mathcal{K}$中，除非向量$a=0$。

凸锥

在尖锥的基础上，若进一步满足$a,a^{\prime}\in\mathcal{K}\Rightarrow a+a^{\prime}\in\mathcal{K}$，则为凸锥。截面可以是任意形状，比如凸多面体、椭圆、超椭圆。

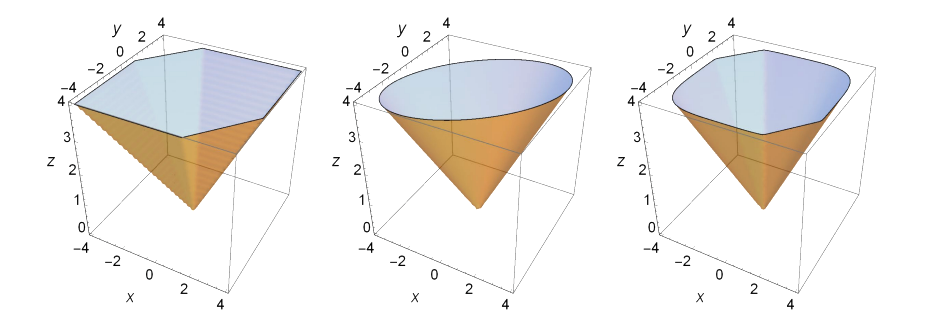
• 多面体锥

  1. 由$Ax\leq b$构成的多面体，其中$x\in\mathbb{R}^n$。
  2. 增加一个维度此时空间$(t,x)\in\mathbb{R}^{n+1}$，构成一个多面体锥$\{t\geq0,Ax\leq bt\}$。
  3. $t=1$时的切片截面是原始多面体。

  

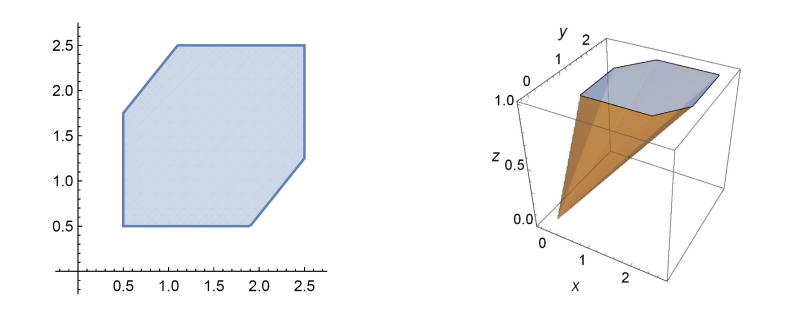
• 椭圆锥

  1. 椭圆$x^\top Px+q^\top x+r\leq0$，其中$P\succ0$且$x\in\mathbb{R}^n$。
  2. 进行仿射变换$\Longleftrightarrow\|Ax+b\|\leq c$。
  3. $\{t\geq0,\|Ax+bt\|\leq ct\}$是$(t,x)\in\mathbb{R}^{n+1}$空间中的一个椭圆锥。
  4. $t=1$时的切片是原始椭圆。

以下三类锥，分别对应LP线性规划、SOCP二次锥规划、SDP半定规划。

常见的锥及其性质

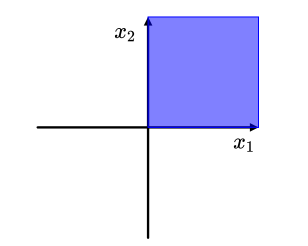
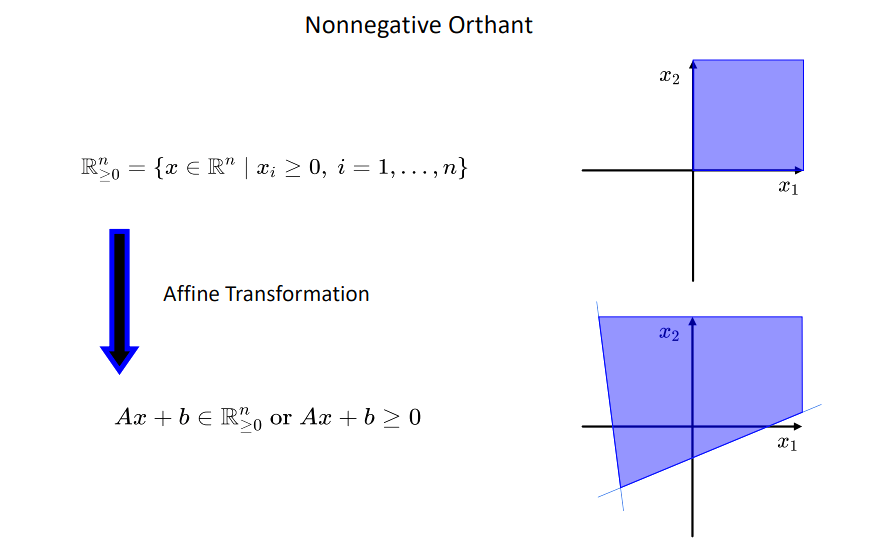
• 非负象限

  $$\mathbb{R}_{\geq0}^n=\{x\in\mathbb{R}^n\mid x_i\geq0,i=1,\ldots,n\}$$

  

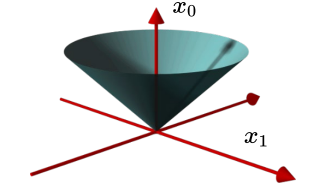
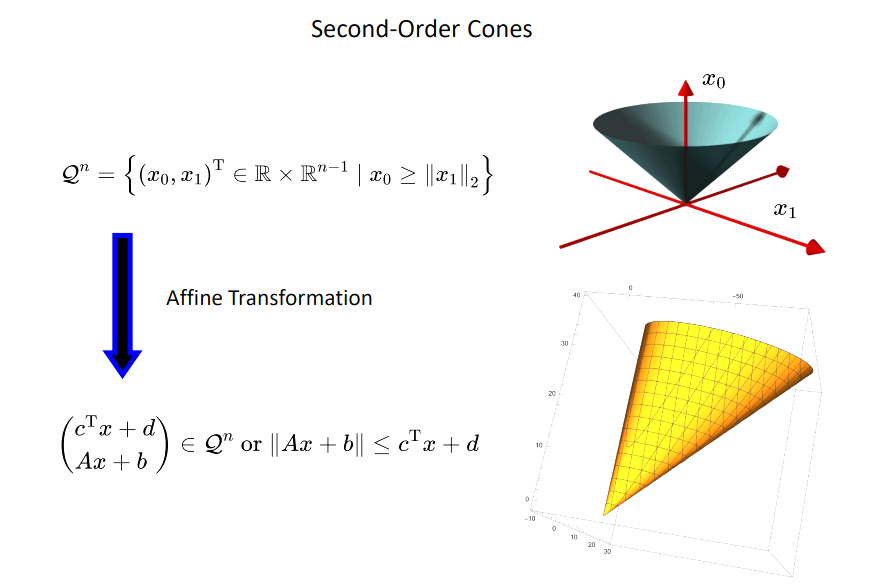
• 二阶锥

  $$\mathcal{Q}^n=\left\{\left(x_0,x_1\right)^{\mathrm{T}}\in\mathbb{R}\times\mathbb{R}^{n-1}\mid x_0\geq\left\|x_1\right\|_2\right\}$$

  

• 半正定锥

  $$\mathcal{S}_{\geq0}^n=\left\{x\in\mathbb{R}^{n(n+1)/2}\mid z^\mathrm{T}\max(x)z\geq0,\forall z\in\mathbb{R}^n\right\}$$

经过仿射变换或旋转，锥可以拓展至如下形式：

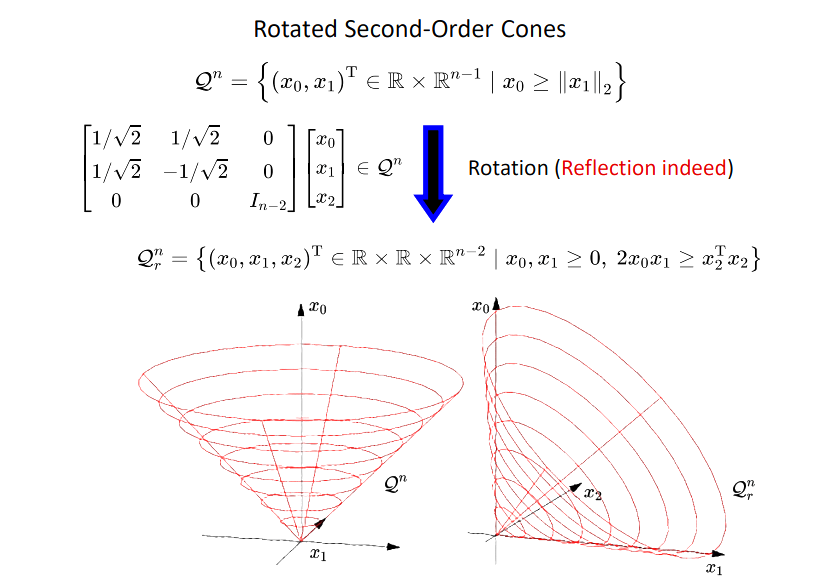
对称锥

$\mathbb{R}_{\geq0}^n,\mathcal{Q}^n,\mathcal{S}_{\geq0}^n$这些锥都是对称的，我们可以将其表示成平方锥（cones of squares）。

• 正象限锥positive orthant

  $$\mathbb{R}_{\geq0}^n=\{x\in\mathbb{R}^n\mid x_i\geq0,i=1,\ldots,n\}=\color{red}\{[y]^2\mid y\in\mathbb{R}^n\}$$

• 二阶锥second-order cone

  $$\mathcal{Q}^n=\left\{\left(x_0,x_1\right)^{\mathrm{T}}\in\mathbb{R}\times\mathbb{R}^{n-1}\mid x_0\geq\left\|x_1\right\|_2\right\}=\color{red}\left\{\frac{1}{\sqrt{2}}\left(y_0^2+y_1^{\mathrm{T}}y_1,2y_0y_1\right)^{\mathrm{T}}\mid\left(y_0,y_1\right)^{\mathrm{T}}\in\mathbb{R}\times\mathbb{R}^{n-1}\right\}$$

• 半正定锥Positive semi-definite cone

  $$\mathcal{S}_{\geq0}^n=\left\{x\in\mathbb{R}^{n(n+1)/2}\mid z^\text{T }{ \max ( x ) }z\geq0,\forall z\in\mathbb{R}^n\right\}=\color{red}\left\{\operatorname{vec}(\operatorname{mat}(y)\operatorname{mat}(y))\mid y\in\mathbb{R}^{n(n+1)/2}\right\}$$

平方操作

锥是对称的当且仅当他是平方时

$$\begin{Bmatrix}x^2:=x\circ x\mid x\in\mathbb{R}^n\end{Bmatrix}$$

必须满足下面特性：

• $x\circ y$是线性的，即$kx\circ y=k(x\circ y)$
• $x\circ y=y\circ x$
• $x^2\circ(y\circ x)=(x^2\circ y)\circ x$
• $\langle x,y\circ z\rangle=\langle x\circ y,z\rangle $

$(\mathbb{R}^n,\circ)$被称为欧几里得乔丹代数Euclidean Jordan algebra。通过代数，可以用统一的方式研究对称锥形成的约束。

圈乘的定义：

• 正象限锥

  $$\mathbb{R}_{\geq0}^n=\{y\circ y\mid y\in\mathbb{R}^n\}$$

  其定义为：

  $$x\circ y:=\operatorname{diag}(x)y$$

• 二阶锥

  $$\mathcal{Q}^n=\left\{y\circ y\mid y=(y_0,y_1)^\text{T}\in\mathbb{R}\times\mathbb{R}^{n-1}\right\}$$

  其定义为：

  $$x\circ y:=\dfrac{1}{\sqrt{2}}\begin{bmatrix}x^Ty\\x_0y_1+y_0x_1\end{bmatrix}$$

• 半正定锥

  $$\mathcal{S}_{\geq0}^n=\left\{y\circ y\mid y\in\mathbb{R}^{n(n+1)/2}\right\}$$

  其定义为：

  $$x\circ y:=\frac12\mathrm{vec}\big(\mathrm{mat}(x)\mathrm{mat}(y)+\mathrm{mat}(y)\mathrm{mat}(x)\big)$$

谱分解

每个欧几里得代数都有其谱分解：

$$x=\sum_{i=1}^\theta\lambda_iq_i$$

其中$\lambda_i$是特征值，$q_i$是特征向量。

分解后的每个特征向量，都满足：

$$q_i^2=q_i,\quad q_i\circ q_{j(\neq i)}=0$$

易知：

• 特征向量是正交的$\langle q_i,q_{j(\neq i)}\rangle=\langle q_i\circ q_i,q_{j(\neq i)}\rangle=\langle q_i,q_i\circ q_{j(\neq i)}\rangle=0$
• 当且仅当一个向量的所有特征值都非负时，该向量在对称锥中。
• 当且仅当一个向量的所有特征值都为正时，该向量在对称锥的内部。

常见锥体的谱分解：

• 正象限锥（positive orthant）

  $$\lambda_i=x_i,\quad q_i=e_i$$

• 二阶锥（second-order cone）

  $$\lambda_i=\frac{x_0\pm\|x_1\|_2}{\sqrt{2}},\quad q_i=\frac1{\sqrt{2}}\begin{bmatrix}1\\\pm x_1/\|x_1\|_2\end{bmatrix}$$

• 半正定锥（second-order cone）

  $$\lambda_i=\lambda_i,\quad q_i=\mathrm{vec}(v_iv_i^\mathrm{T})$$

  其中$\lambda_i$和$v_i$是$mat(x)$的特征值和特征向量。

对称锥的自对偶性

锥$\mathcal{K}$的对偶锥记为$\mathcal{K}^*$，即与中$\mathcal{K}$任意元素$y$的内积大于0的$x$的集合，如下所示：

$$\mathcal{K}^*=\{x\mid\langle x,y\rangle\geq0,\forall y\in\mathcal{K}\}$$

因此对称锥的对偶锥是他本身，即$\mathcal{K}^*=\mathcal{K}$。

对称锥的应用

回顾一下之前约束优化问题的分类：

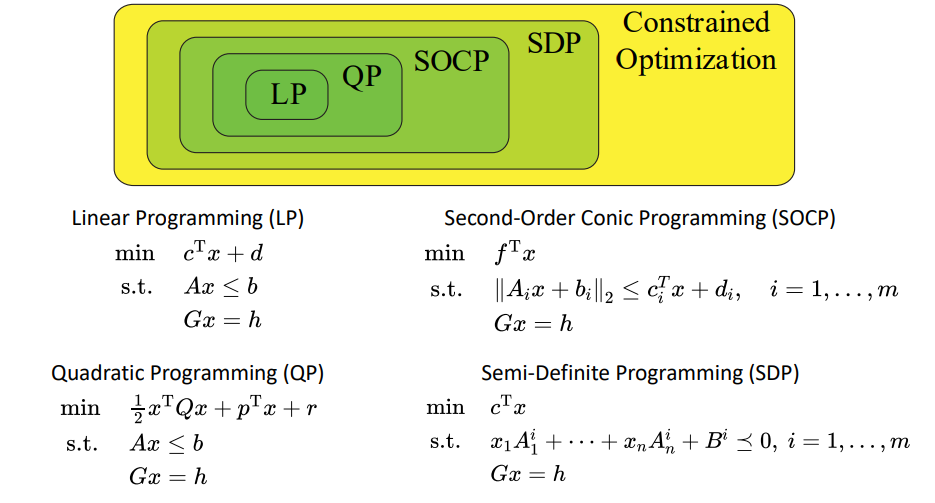
上面的包含关系是怎么来的呢？

1. LP写成QP形式

   

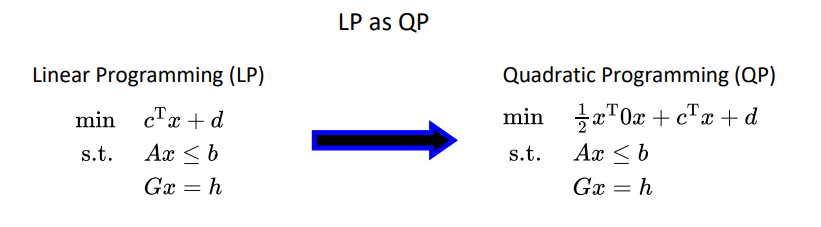
2. QP写成SOCP的形式

   

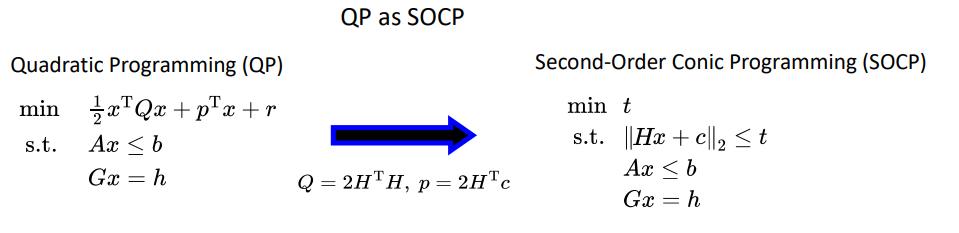
3. SOCP写成SDP形式

   

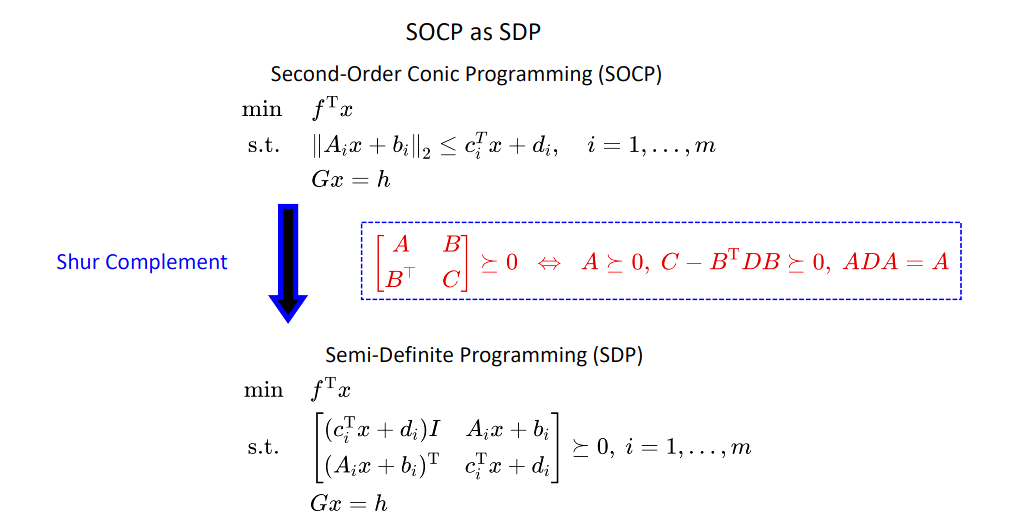
二阶锥规划问题是一类对称锥规划问题，另外有一部分半定规划问题也是对称锥规划问题，也就是说这两类规划问题的不等式约束条件都可以表示为解处于一个对称锥内的形式。SDP是最广泛的对称凸锥优化问题！许多优化问题可以通过 Lasserre hierarchy 结构简化为SDP。

锥增广拉格朗日函数

数值优化笔记（三）：锥规划问题

推导

对称锥规划问题可以表示成：

$$\begin{aligned} &\min_{x\in\mathbb{R}^{n}} c^{\mathrm{T}}x \\ &\mathrm{s.t.} A_{i}x+b_{i}\in\mathcal{K}_{i},i=1,\ldots,m \\ &Gx=h \end{aligned}$$

由前面我们可以根据对称锥的概念，所有对称锥内部的向量，可以表示为一个$\mathbb{R}^n$向量关于圈乘

$$\begin{aligned} &\min_{x,s} c^{\mathrm{T}}x \\ &\mathbf{s.t.} A_ix+b_i={s_i\circ s_i},\mathrm{~}i=1,\ldots,m \\ &Gx=h \end{aligned}$$

因此我们可以构建对于等式约束的拉格朗日函数如下：

$$\mathcal{L}_\rho(x,s,\lambda,\nu):=c^\mathrm{T}x+\frac{\rho}{2}\begin{Vmatrix}Gx-h+\frac{\lambda}{\rho}\end{Vmatrix}^2+\frac{\rho}{2}\sum_{i=1}^m\begin{Vmatrix}A_ix+b_i-s_i\circ s_i+\frac{\nu_i}{\rho}\end{Vmatrix}^2$$

$$\begin{cases}x^{k+1}=\arg\min_{x,s}\mathcal{L}(x^k,s^k,\lambda^k,\mu^k,\rho^k)\\\lambda^{k+1}=\lambda^k+\rho^k(Gx^{k+1}-h)\\\mu_i^{k+1}=\mu_i^k+\rho^k(A_ix^{k+1}+b_i-s_i\circ s_i)\\\rho^{k+1}=\min(\rho^k+\gamma\rho^k,\beta)\end{cases}$$

其中，$k$代表迭代轮数，$\lambda$和$\mu_i$是拉格朗日乘子，$\rho$是惩罚系数。当时上述式子中多出来一个变量$s$。下面是将其消去的推导过程：

对于$\min_{x,s}\mathcal{L}$问题，由于$s$只和最后一项有关，因此对于任何一个$x$，都可以很容易地求解出对应的最优的$s^*$的取值。只需要求解下面的优化问题即可，这里可以将$x$看作常量：

$$\begin{aligned}\min_s\frac{1}{2}\rho\sum_{i=1}^m||A_ix+b_i-s_i\circ s_i+\frac{\mu_i}{\rho}||^2\end{aligned}$$

上述式子中$A_{i}x+b_{i}+\frac{\mu_{i}}{\rho}$与$s$无关，并且$s_i$之间也无关联。因此上述式子可以写成：

$$\min_{s}||v-s_i\circ s_i||^2$$

其中$v=A_{i}x+b_{i}+\frac{\mu_{i}}{\rho}$。

即

$$\min_s\left\|v-s_i\circ s_i\right\|^2=\min_{x\in\mathcal{K}}\left\|v-x\right\|^2$$

我们从几何角度去理解这个问题，事实上这个问题的最优解就是找到向量$v$在对称锥$\mathcal{K}$上的投影向量，此时$v-x$与锥垂直，即距离最近。如下图所示：

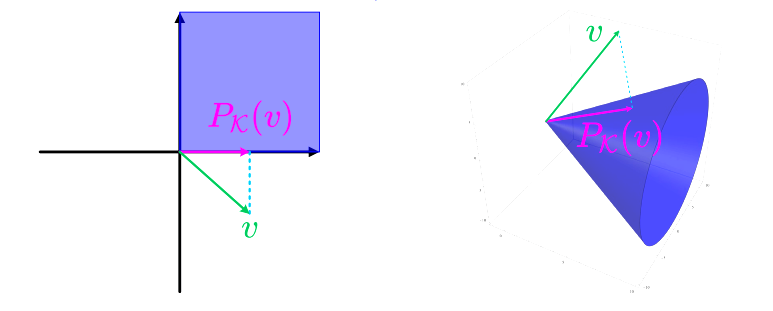
我们用$P_{\kappa}(v)$表示向量$v$在$\mathcal{K}$上的投影，则可以得到下式：

$$\min_s\left\|v-s_i\circ s_i\right\|^2=\left\|P_{\mathcal{K}}\left(-v\right)\right\|^2$$

且根据对称锥的另一个特性Moreau decomposition（此处不具体推导，看下图即可）:

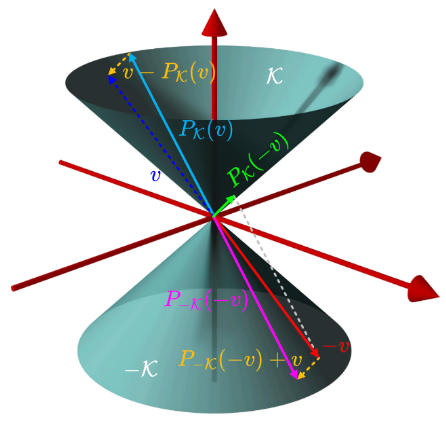
由上可得：

$$v-P_{\mathcal{K}}(v)=-P_{\mathcal{K}}(-v)$$

最终我们可以得到：

$$\min_s\left\|v-s_i\circ s_i\right\|^2=\left\|P_{\mathcal{K}}(-v)\right\|^2$$

所以原拉格朗日函数：

$$\min_s\mathcal{L}_\rho(x,s,\lambda,\nu)=c^\mathrm{T}x+\frac\rho2\begin{Vmatrix}Gx-h+\frac\lambda\rho\end{Vmatrix}^2+\frac\rho2\sum_{i=1}^m\begin{Vmatrix}P_{\mathcal{K}_i}\big(-A_ix-b_i-\frac{\nu_i}\rho\big)\end{Vmatrix}^2$$

我们用$\mu=-v$，因此对称锥的增广拉格朗日量：

$$\mathcal{L}_\rho(x,\lambda,\mu):=c^\mathrm{T}x+\frac\rho2\Big\{\left\|Gx-h+\frac\lambda\rho\right\|^2+\sum_{i=1}^m\left\|P_{\mathcal{K}_i}\left(\frac{\mu_i}\rho-A_ix-b_i\right)\right\|^2\Big\}-\color{gray}\frac1{2\rho}\Big\{\|\lambda\|^2+\|\mu\|^2\Big\}$$

其原函数下降和对偶函数上升过程与PHR-ALM相同。

特别的，对偶变量的更新如下：$(-\mu_i)\leftarrow(-\mu_i)+\rho(A_ix+b-s_i\circ s_i)$，其中$s_{i}\circ s_{i}=P_{\mathcal{K}}(A_{i}x+b_{i}+\frac{-\mu_{i}}{\rho})$。

再运用一次莫罗分解，可以得到：

$$\mu_i\leftarrow P_{\mathcal{K}_i}(\mu_i-\rho(A_ix+b_i))$$

总结如下

原问题为：

$$\begin{aligned} &\min_{x\in\mathbb{R}^{n}} c^{\mathrm{T}}x \\ &\mathrm{s.t.} A_{i}x+b_{i}\in\mathcal{K}_{i},i=1,\ldots,m \\ &Gx=h \end{aligned}$$

其增广拉格朗日函数为：

$$\mathcal{L}_\rho(x,\lambda,\mu):=c^\mathrm{T}x+\frac\rho2\Big\{\left\|Gx-h+\frac\lambda\rho\right\|^2+\sum_{i=1}^m\left\|P_{\mathcal{K}_i}\left(\frac{\mu_i}\rho-A_ix-b_i\right)\right\|^2\Big\}-\color{gray}\frac1{2\rho}\Big\{\|\lambda\|^2+\|\mu\|^2\Big\}$$

其中$\rho > 0, \mu_i \in \mathcal{K}_i$，然后进行迭代

$$\begin{cases}x\leftarrow\operatorname{argmin}_x\mathcal{L}_\rho(x,\lambda,\mu)\\\lambda\leftarrow\lambda+\rho(Gx-h)\\\mu_i\leftarrow P_{\mathcal{K}_i}\big(\mu_i-\rho(A_ix+b_i)\big)\\\rho\leftarrow\min[(1+\gamma)\rho,~\beta]\end{cases}$$

• 初始化$\rho_{\mathrm{ini}}=1,\lambda_{\mathrm{ini}}=\mu_{\mathrm{ini}}=0,\gamma=1,\beta=10^3$
• 迭代终止条件$\max\left[\left\|Gx-h\right\|_\infty,\max_i\left\|\frac{\mu}{\rho}-P_{\mathcal{K}_i}\big(\frac{\mu}{\rho}-A_ix-b_i\big)\right\|_\infty\right]<\epsilon_{\mathrm{cons}},\left\|\nabla_x\mathcal{L}_\rho(x,\lambda,\mu)\right\|_\infty<\epsilon_{\mathrm{prec}}$

锥投影的计算

根据谱分解的概念，任意一个向量都可以分解为：

$$x=\sum_{i=1}^\theta\lambda_iq_i$$

对于不同的锥$q_i$也是不同的，投影操作可以被描述为：

$$\mathrm{P}_{\mathcal{K}}(x)=\sum_{i=1}^\theta\max(\lambda_i,0)q_i$$

上述式子的含义是，把向量$x$按照$q_i$进行分解，并将所有小于0的特征值设置为0，然后再进行线性组合。即把分解后所有特征值为负数的部分舍弃。

半光滑牛顿方法

锥增广拉格朗日算法的迭代过程中需要求解一个无约束优化问题：

$$\min_{x}\mathcal{L}_{\rho}(x,\lambda,\mu)=c^{\mathrm{T}}x+\frac{\rho}{2}\Big\{\left\|Gx-h+\frac{\lambda}{\rho}\right\|^{2}+\sum_{i=1}^{m}\left\|P\chi_{i}\left(\frac{\mu_{i}}{\rho}-A_{i}x-b_{i}\right)\right\|^{2}\Big\}$$

这个问题中，目标函数是一个一阶连续可微的凸函数，但无法保证二阶连续可微，因此其Hessian未必是连续的。因此，上述问题可以用梯度下降法和拟牛顿法进行求解，但无法用一般的牛顿方法进行求解。

使用拟牛顿法求解时，

该子问题就是增广拉格朗日函数对$x$求最小值，即

$$\mathcal{L}_\rho(x,\lambda,\mu)\text{w.r.t.}x$$

其梯度和Hessian矩阵是

$$g=\nabla_x\mathcal{L}_\rho(x,\lambda,\mu),H=\nabla_x^2\mathcal{L}_\rho(x,\lambda,\mu)$$

圆锥增广拉格朗日函数的凸性保证了

$$H\succeq0$$

所以我们是否可以使用拟牛顿法进行下列更新？

$$(H+\epsilon I)d=-g,\mathrm{~}\epsilon=\min(1,\|g\|_\infty)$$

在二阶连续可微的地方当然可以，但是当最优解在边界上（锥的边缘），很有可能在Hessian不存在的区域，可以采用如下介绍的半光滑的牛顿方法。

半光滑的定义：

定义一个向量函数：$F(x):\mathbb{R}^n\to\mathbb{R}^n$，那么当$F(x)$在$x$处方向可导，且

$$\lim_{d\in\mathbb{R}^n,d\to0}\frac{||F(x+d)-F(x)-J(d)d||}{||d||}=0, \forall J(d)=\partial F(x+d)$$

则称$F(x)$在$x$处是半光滑的。

如果再进一步，若满足下列条件，它是强半光滑的

$$\lim_{d\in\mathbb{R}^n,\mathrm{~}d\to0}\frac{\|F(x+d)-F(x)-J(d)d\|}{\|d\|^2}<\infty,\mathrm{~}\forall J(d)\in\partial F(x+d)$$

B次微分的定义：

$\partial_BF(x)=\{\lim_{k\to\infty}F'(x^k)|x^k\in D_F,x^k\to x\}$，其中$D_F$代表的是$x^k$的可行域。B次微分和一般次微分的关系是：$\partial F(x)=\operatorname{conv}(\partial_BF(x))$，其中$conv$代表取凸包的操作。

半光滑牛顿方法：

如果$F(x):\mathbb{R}^n\mapsto\mathbb{R}^n$是半光滑的，则$J(x)\in\partial_BF(x)$是非奇异的

$$x^{k+1}=x^k-J(x^k)^{-1}F(x^k)$$

也就是说，用B次微分代替Hessian矩阵参与牛顿迭代，这就是所谓的半光滑牛顿法。

上述迭代可以达到局部超线性收敛

$$F(x)=0$$

如果$F(x):\mathbb{R}^n\mapsto\mathbb{R}^n$是强光滑的，迭代可以到达局部二次收敛

$$g(x):=\nabla_x\mathcal{L}_\rho(x,\lambda,\mu)$$

锥增广拉格朗日函数的梯度是强半光滑的，因为它是分段C2。
因此，我们可以如下计算半平滑牛顿步来进行无约束优化

$$\begin{aligned} &(H+{\epsilon}I)d=-{g} \\ &g=\nabla_x\mathcal{L}_\rho(x,\lambda,\rho) \\ &H\in\partial_B\nabla_x\mathcal{L}_\rho(x,\lambda,\rho) \\ &\epsilon=\min(1,\|g\|_\infty)/10 \end{aligned}$$

如何计算梯度和B次微分呢？

梯度可以直接进行计算：

$$\nabla_x\mathcal{L}_\rho(x,\lambda,\mu)=c+G^\mathrm{T}(\lambda+\rho(Gx-h))-\sum_{i=1}^mA_i^\mathrm{T}P_{\mathcal{K}_i}(\mu-\rho(A_ix+b_i))$$

所谓的广义Hessian，即梯度的B次微分如下式：

$$\partial_B\nabla_x\mathcal{L}_\rho(x,\lambda,\mu)=\rho\Big(G^\mathrm{T}G+\sum_{i=1}^mA_i^\mathrm{T}\partial_BP_{\mathcal{K}_i}(\mu-\rho(A_ix+b_i))A_i\Big)$$

特别的，对于SOCP，B次微分可以选择为：

$$\partial_{B} P_{\mathcal{K}_{i}}(x) \ni\left\{\begin{array}{ll} I_{n} & \left\|x_{2}\right\| \leq x_{1}, \\ 0 & \left\|x_{2}\right\| \leq-x_{1}, \\ \left(\begin{array}{cc} \frac{1}{2} & \frac{x_{2}^{\mathrm{T}}}{2\left\|x_{2}\right\|} \\ \frac{x_{2}}{2\left\|x_{2}\right\|} & \frac{x_{1}+\left\|x_{2}\right\|}{2\left\|x_{2}\right\|} I_{n-1}-\frac{x_{1} x_{2} x_{2}^{\mathrm{T}}}{2\left\|x_{2}\right\|^{3}} \end{array}\right) & \left\|x_{2}\right\|>\left|x_{1}\right| . \end{array}\right.$$

应用：时间最优路径规划（TOPP）

路径$q$由弧长变量$s$参数化，TOPP是在给定的平滑路径上生成时间剖面，路径的持续时间应该尽可能地短。

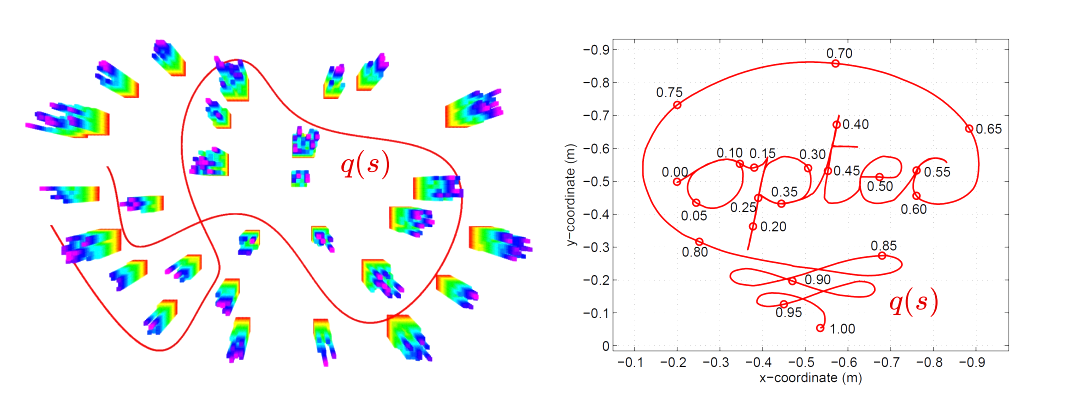
使用弧长参数s来对路径进行参数化，s的值表示的是距离路径起点所走过的距离。与速度加速度的概念类似：

$${a(s)}=\frac{\mathrm{d}^2s}{\mathrm{d}t^2},{b(s)}=\left(\frac{\mathrm{d}s}{\mathrm{d}t}\right)^2$$

根据运动学基础公式

$$v_s^2-v_0^2=2as$$

距离参数化速度的平方与二阶导数成线性关系

$$b^{\prime}(s)=2a(s)$$

所以，目标函数（时间最优）

$$T=\int_0^T1\mathrm{d}t=\int_{s(0)}^{s(T)}\frac{1}{\mathrm{d}s/\mathrm{d}t}\mathrm{d}s=\int_0^L\frac{1}{\mathrm{d}s/\mathrm{d}t}\mathrm{d}s=\int_0^L\frac{1}{\sqrt{b(s)}}\mathrm{d}s$$

真实速度

$$\frac{\mathrm{d}q}{\mathrm{d}t}=q'(s)\frac{\mathrm{d}s}{\mathrm{d}t}=q'(s)\sqrt{b(s)}$$

真实加速度

$$\frac{\mathrm{d}^2q}{\mathrm{d}t^2}=q''(s)\left(\frac{\mathrm{d}s}{\mathrm{d}t}\right)^2+q'(s)\frac{\mathrm{d}^2s}{\mathrm{d}t^2}=q''(s)b(s)+q'(s)a(s)$$

更重要的是，我们仅考虑向前移动的情况，因此$b(s)\geq0$应该严格成立，并仅在某个或某几个瞬间为0。

因此我们将这个简单的TOPP问题描述为：

$$\begin{aligned} \min_{a(s),b(s)}& \int_{0}^\frac{1}{\sqrt{b(s)}}\mathrm{d}s \\ \mathrm{s.t.}& b(s)\geq0, \forall s\in[0,L], \\ &b'(s)=2a(s), \forall s\in[0,L], \\ &\left\|q^{\prime}(s)\sqrt{b(s)}\right\|_{\infty}\leq v_{max}, \forall s\in[0,L], \\ &\left\|q^{\prime\prime}(s)b(s)+q^{\prime}(s)a(s)\right\|_\infty\leq{a_{max}},\quad\forall s\in[0,L], \\ &b(0)={b_0},b(L)={b_L}. \end{aligned}$$

将上述问题变为SOCP

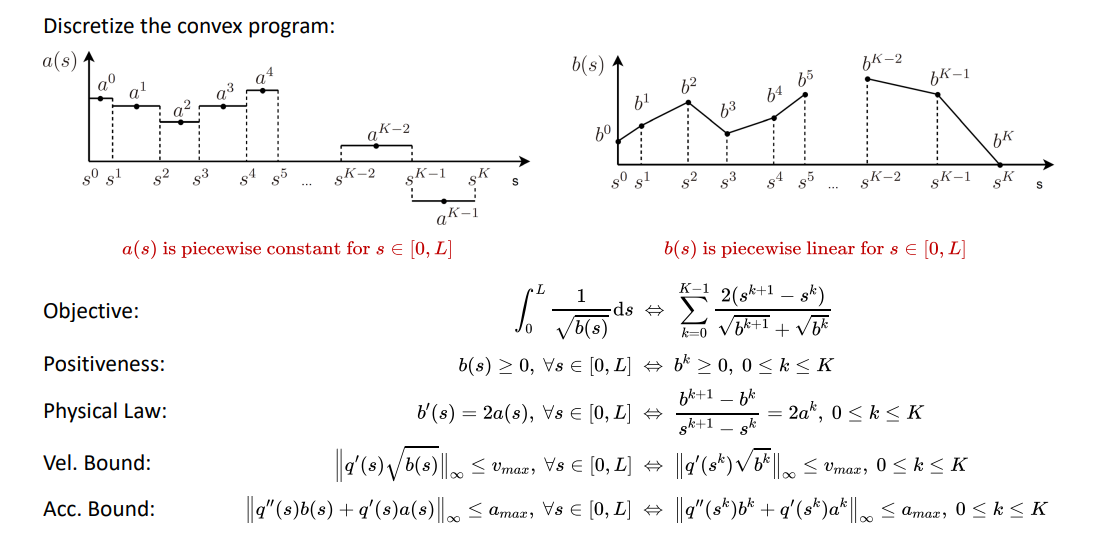
其中是引入一些变量进行一些缩放，将表达形式便形成SOCP的形式。
增加隐变量$c^k, d^k$，满足：

$$c^k\leq\sqrt{b^k},\quad\frac1{c^{k+1}+c^k}\leq d^k$$

则通过缩放可以得到$\frac1{\sqrt{b^{k+1}}+\sqrt{b^k}}\leq d^k$，以上每步等号都可以取到，则$\min\frac1{\sqrt{b^{k+1}}+\sqrt{b^k}}\iff\min d^k$，同时$b^k, c^k, d^k$需要满足上面两个约束，即：

$$\begin{aligned} \begin{Vmatrix}2\\c^{k+1}+c^k-d^k\end{Vmatrix}_2 &\leq c^{k+1}+c^k+d^k,\quad0\leq k\leq K-1, \\ \begin{Vmatrix}2c^k\\b^k-1\end{Vmatrix}_2 &\leq b^k+1,\quad0\leq k\leq K. \end{aligned}$$

综上所述TOPP转化SOCP为：

目标函数：

$$\min_{a^k,b^k,c^k,d^k}\sum_{k=0}^{K-1}2(s^{k+1}-s^k)d^k$$

锥约束：

$$\begin{aligned} \begin{Vmatrix}2\\c^{k+1}+c^k-d^k\end{Vmatrix}_2 &\leq c^{k+1}+c^k+d^k,\quad0\leq k\leq K-1, \\ \begin{Vmatrix}2c^k\\b^k-1\end{Vmatrix}_2 &\leq b^k+1,\quad0\leq k\leq K. \end{aligned}$$

等式约束：

$$\begin{aligned} &2(s^{k+1}-s^k)a^k+b^k-b^{k+1}=0,(0\leq k\leq K-1) \\ &\left\|q^{\prime}(s^0)\right\|_2^2b^0=v_{start}^2 \\ &\left\|q^{\prime}(s^k)\right\|_2^2b^K=v_{end}^2 \end{aligned}$$

不等式约束：

$$\begin{aligned} &-b_k\leq0,(0\leq k\leq K) \\ &\left(\left(q_{y}^{\prime}\left(s^{k}\right)\right)^{2}+\left(q_{x}^{\prime}\left(s^{k}\right)\right)^{2}\right)b^{k}-v_{max}^{2}\leq0,(0\leq k\leq K) \\ &q_x^{\prime\prime}\left(s^k\right)b^k+q_x^{\prime}\left(s^k\right)a^k-a_{max}\leq0,(0\leq k\leq K-1) \\ &q_y^{\prime\prime}(s^k)b^k+q_y^{\prime}(s^k)a^k-a_{max}\leq0,(0\leq k\leq K-1) \\ &-q_x^{\prime\prime}(s^k)b^k-q_x^{\prime}(s^k)a^k-a_{max}\leq0,(0\leq k\leq K-1) \\ &-q_y^{\prime\prime}(s^k)b^k-q_y^{\prime}(s^k)a^k-a_{max}\leq0,(0\leq k\leq K-1) \end{aligned}$$

作业

作业一：证增广拉格朗日函数是关于$x$的凸函数

原问题是一个凸优化问题：

$$\begin{array}{rl}\min&f(x)\\\text{s.t.}&g(x)\leq0\\&h(x)=0\end{array}$$

则我们可得

1. $f(x)$和$g(x)$都是凸函数，$h(x)$是仿射函数（既凸又凹）。

且

2. 凸函数充要条件

$$f\big(\alpha x+(1-\alpha)y\big)\leq\alpha f(x)+(1-\alpha)f(y),\forall x,y\in domf,\alpha\in(0,1)$$

3. 凸函数加凸函数还是凸函数。$f_1\ldots f_n$为凸函数，$w_{i}\geq0$则$f=\sum_i^nw_if_i$为凸函数。

4. 若$f$为$I$上的凸函数，$g$在$J(f(I)⊂J)$上递增，且凸性相同，$g◦f$在$I$上有相同的凸性。

上述为证明所用到的定理，其中3和4均可由2推导得到。

证：

增广拉格朗日函数为

$$\mathcal{L}_\rho(x,\lambda,\mu):=f(x)+\frac{\rho}{2}\left\{\left\|h(x)+\frac{\lambda}{\rho}\right\|^2+\left\|\max\left[g(x)+\frac{\mu}{\rho},0\right]\right\|^2\right\}-\frac{1}{2\rho}\left\{\|\lambda\|^2+\|\mu\|^2\right\}$$

其中$\rho>0,\mu\succeq0$

• $f(x)$为凸函数，$\frac1{2\rho}\big\{\|\lambda\|^2+\|\mu\|^2\big\}$与$x$无关。

• 当$h(x)+\frac{\lambda}{\rho}\ge 0$时，$\left|\left|\cdot\right|\right|^2$在$[0, +\infty]$上单调递增且为凸函数。由定理4我们可得，$\left\|h(x)+\frac\lambda\rho\right\|^2$为凸函数。

• 与上同理，易得$\max\left[g(x)+\frac{\mu}{\rho},0\right]$为凸函数且$\max\left[g(x)+\frac{\mu}{\rho},0\right] \ge 0$，$\left|\left|\cdot\right|\right|^2$在$[0, +\infty]$上单调递增且为凸函数。由定理4我们可得，$\left\|\max\left[g(x)+\frac\mu\rho,0\right]\right\|^2$为凸函数。

综上所述，增广拉格朗日函数$\mathcal{L}_\rho(x,\lambda,\mu)$是关于$x$的凸函数。

作业二：低维半正定的二次规划问题

原问题：

$$\begin{gathered} \\ \operatorname*{min}_{x\in\mathbb{R}^{n}}{\frac{1}{2}}x^{\mathrm{T}}M_{\mathcal{Q}}x+c_{\mathcal{Q}}^{\mathrm{T}}x,\mathrm{s.t.}A_{\mathcal{Q}}x\leq b_{\mathcal{Q}} \\ \mathrm{where},M_{\mathcal{Q}}\succeq0. \end{gathered}$$

这是一个半正定的二次规划问题。

原求解器只能求解严格正定的二次规划问题，所以我们将其构建成一个严格正定的二次规划问题。

给原目标函数加上一个正则项，变为

$$\operatorname*{min}_{x\in\mathbb{R}^{n}}{\frac{1}{2}}x^{\mathrm{T}}M_{\mathcal{Q}}x+c_{\mathcal{Q}}^{\mathrm{T}}x+\frac{1}{2\rho}\left\|x-\bar{x}\right\|^2$$

展开得

$$\operatorname*{min}_{x\in\mathbb{R}^{n}}{\frac{1}{2}}x^{\mathrm{T}}M_{\mathcal{Q}}x+c_{\mathcal{Q}}^{\mathrm{T}}x+\frac{1}{2\rho}(x^{\mathrm{T}}x+\bar{x}^{\mathrm{T}}\bar{x}-2\bar{x}^{\mathrm{T}}x)$$

即

$$\operatorname*{min}_{x\in\mathbb{R}^{n}}{\frac{1}{2}}x^{\mathrm{T}}(M_{\mathcal{Q}}+\frac{1}{\rho})x+(c_{\mathcal{Q}}-\frac{1}{\rho}\bar{x})^{\mathrm{T}}x+\frac{1}{2\rho}\bar{x}^{\mathrm{T}}\bar{x}$$

这样上述问题就会变成严格正定的二次规划问题

1. 初始化$\bar{x}$，给定$\delta$

2. 求出下列二次规划问题的解$x^*_{i}$

$$\operatorname*{min}_{x\in\mathbb{R}^{n}}{\frac{1}{2}}x^{\mathrm{T}}(M_{\mathcal{Q}}+\frac{1}{\rho})x+(c_{\mathcal{Q}}-\frac{1}{\rho})^{\mathrm{T}}x$$

4. 判断$\left|x-\bar{x}\right|^2 \le \delta $，若满足条件迭代结束；若不满足继续迭代。
5. $\bar{x} \gets x^*_{i}$，转到步骤2。

代码见文件task2所示。

运行

1. cd chapter04/task2
2. 编译
3. 运行可执行文件./sdqp_example

结果如下：

作业三：SOCP求解

原问题：

$$\begin{aligned} &\min_{x\in\mathbb{R}^{n}} f^{\mathrm{T}}x \\ &\mathrm{s.t.} \left \|{Ax+b}\right \|_2 \leq c^{\mathrm{T}}x+d \end{aligned}$$

其中

$$A=\begin{bmatrix}7&&&&&&&\\&6&&&&&&\\&&5&&&&&\\&&&4&&&&\\&&&&3&&&\\&&&&&2&&\\&&&&&&1\end{bmatrix},b=\begin{bmatrix}1\\3\\5\\7\\9\\11\\13\end{bmatrix},c=\begin{bmatrix}1\\0\\0\\0\\0\\0\\0\end{bmatrix},f=\begin{bmatrix}1\\2\\3\\4\\5\\6\\7\end{bmatrix},d=1$$

我们构建一个二阶锥

$$\mathcal{K}=\left\{\left(y_0,y_1\right)^{\mathrm{T}}\in\mathbb{R}\times\mathbb{R}^{n-1}\mid y_0\geq\left\|y_1\right\|_2\right\}$$

其中$y_0=c^Tx+d,y_1=Ax+b$。

所以原问题变为：

$$\min_xf^Tx,s.t.A_ix+b_i\in \mathcal{K}$$

其中

$$A_i=\begin{bmatrix}c^T\\A\end{bmatrix},b_i=\begin{bmatrix}d\\b\end{bmatrix}$$

根据前文锥的增广拉个朗日函数可得：

$$L_\rho(x,\mu)=f^Tx+\frac{\rho}{2}\left(\left\|P_{\mathcal{K}}(\frac{\mu}{\rho}-A_ix-b_i)\right\|^2\right)$$

迭代

$$\begin{cases}x\leftarrow\operatorname{argmin}_x\mathcal{L}_\rho(x,\lambda,\mu)\\ \mu_i\leftarrow P_{\mathcal{K}_i}\big(\mu_i-\rho(A_ix+b_i)\big)\\\rho\leftarrow\min[(1+\gamma)\rho,~\beta]\end{cases}$$

其中$x\leftarrow\operatorname{argmin}_x\mathcal{L}_\rho(x,\lambda,\mu)$可使用前文的半光滑牛顿方法求得。

具体代码见task3

运行：

1. cd chapter04/task3
2. 编译
3. 运行可执行文件./socp_example

结果如下：