机器人中的数值优化（三）

文档维护：Arvin

网页部署：Arvin

▶

写在前面：本文内容是作者在深蓝学院机器人中的数值优化学习时的笔记，作者按照自己的理解进行了记录，如果有错误的地方还请执政。如涉侵权，请联系删除。

有约束优化（笔记）

分类

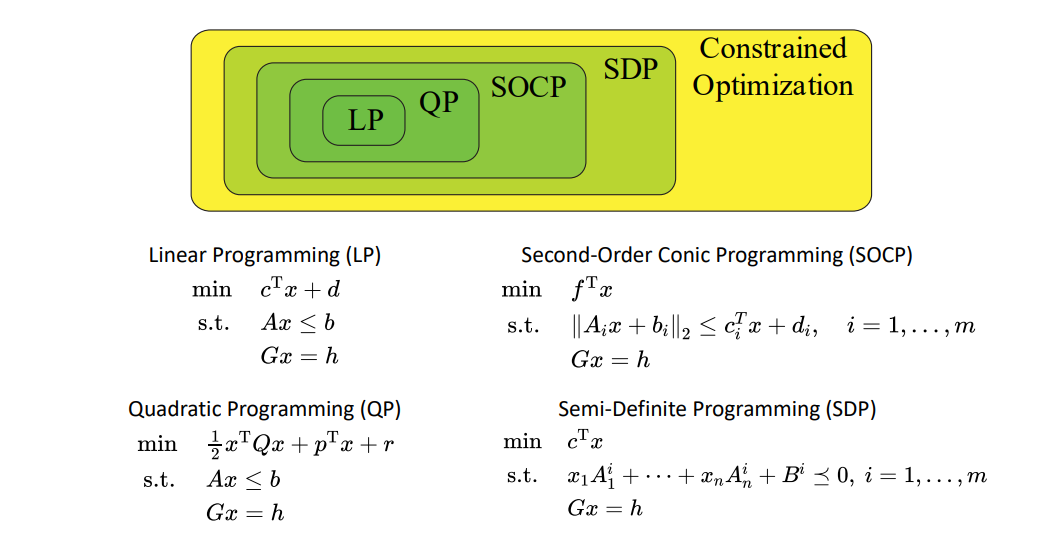
低维线性规划（LP）

目标函数：

$$f(x_1,x_2\ldots x_d)=c_1x_1+c_2x_2+\cdots+c_dx_d$$

约束：

$$\begin{array}{l} a_{1,1} x_{1}+\cdots+a_{1, d} x_{d} \leqslant b_{1} \\ a_{2,1} x_{1}+\cdots+a_{2, d} x_{d} \leqslant b_{2} \\ a_{n, 1} x_{1}+\cdots+a_{n, d} x_{d} \leqslant b_{n} \\ \end{array}$$

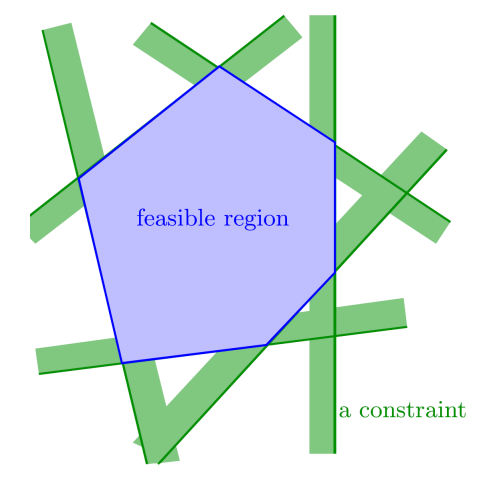
每个约束表示$\mathbb{R}^d$中的一个半空间，半空间的交集形成可行域，可行域是$\mathbb{R}^d$中的凸多面体。

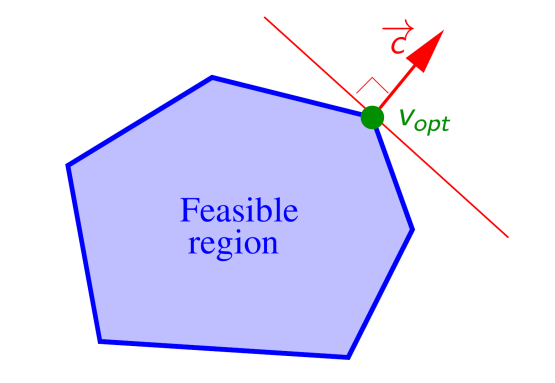
我们使$\vec{c}=(c_1,c_2,\ldots c_d)$（即目标函数梯度），沿此方向最前的那个点$v_{opt}$就是LP问题的解。

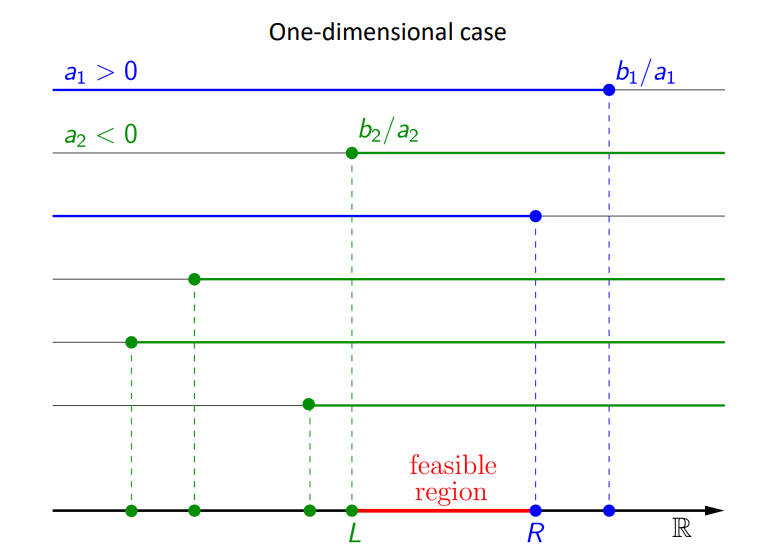
一维

目标函数：

$$f(x)=cx$$

约束：

$$\begin{array}{l}a_1x\leqslant b_1\\a_2x\leqslant b_2\\\vdots&\vdots\\a_nx\leqslant b_n\end{array}$$

二维：

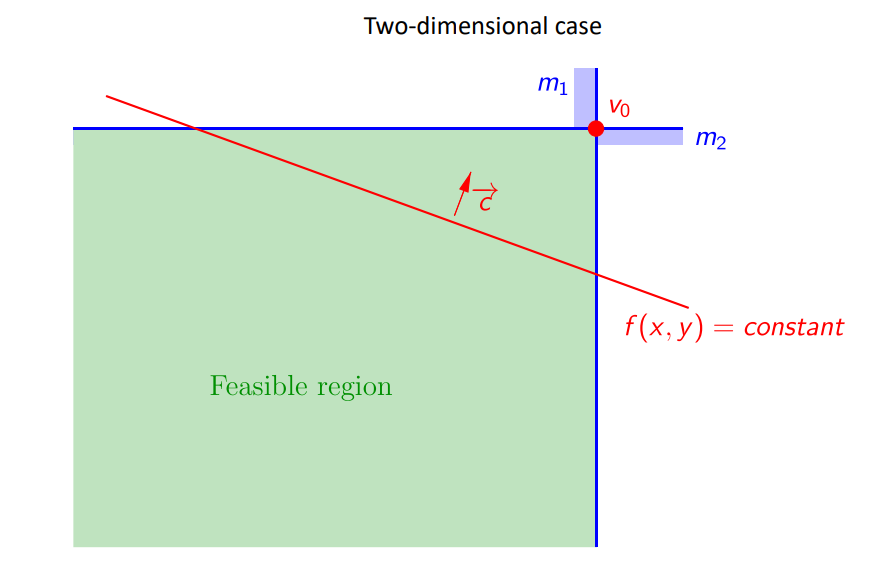
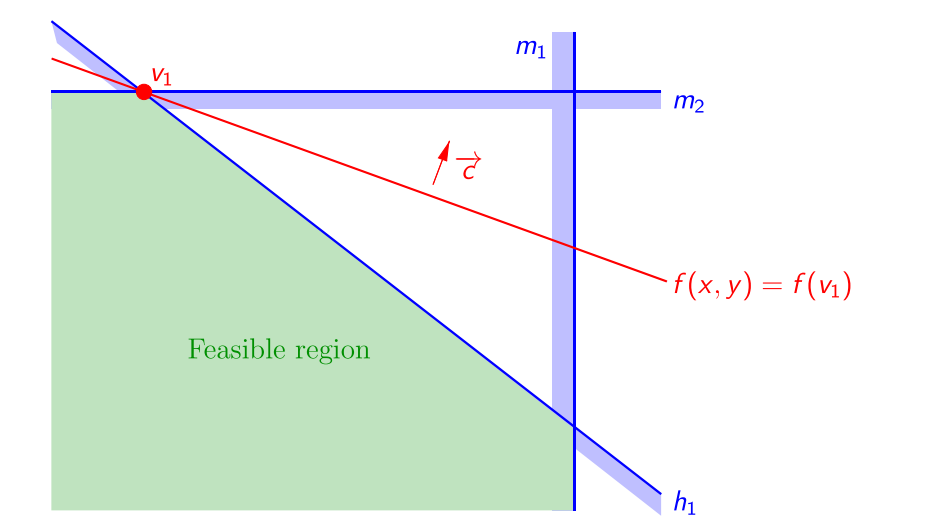
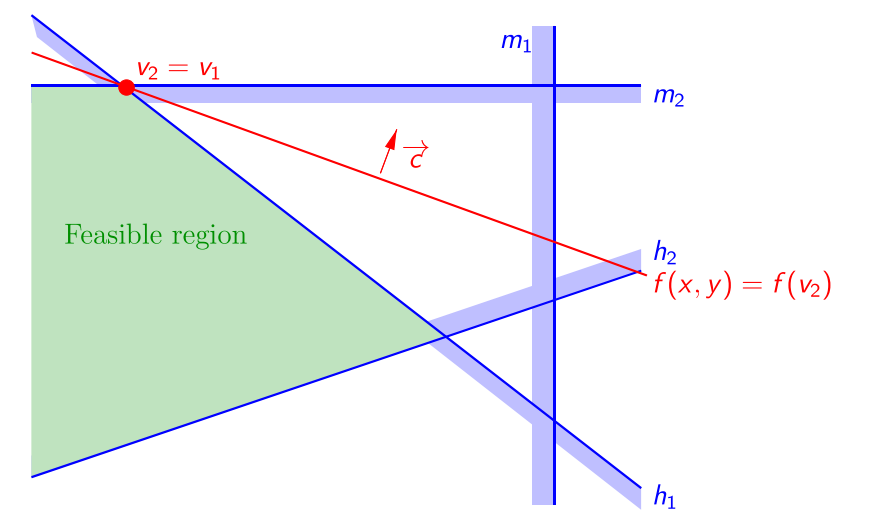
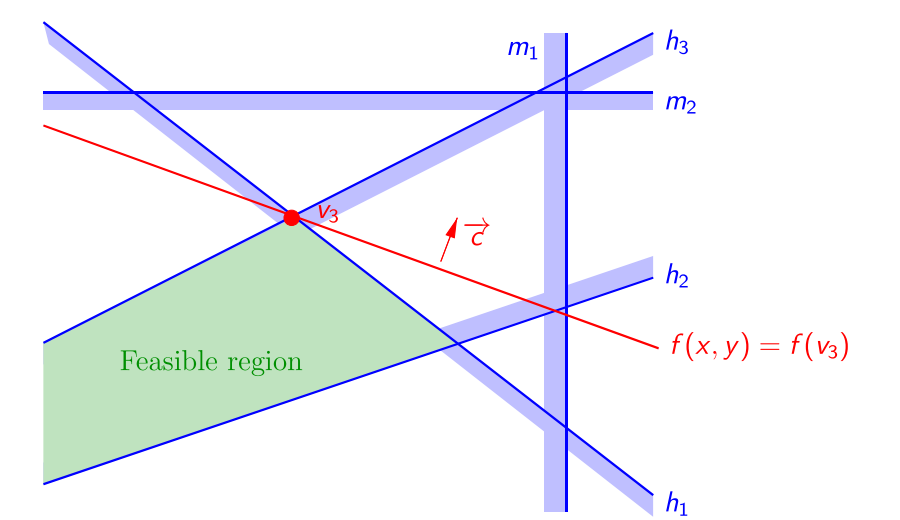
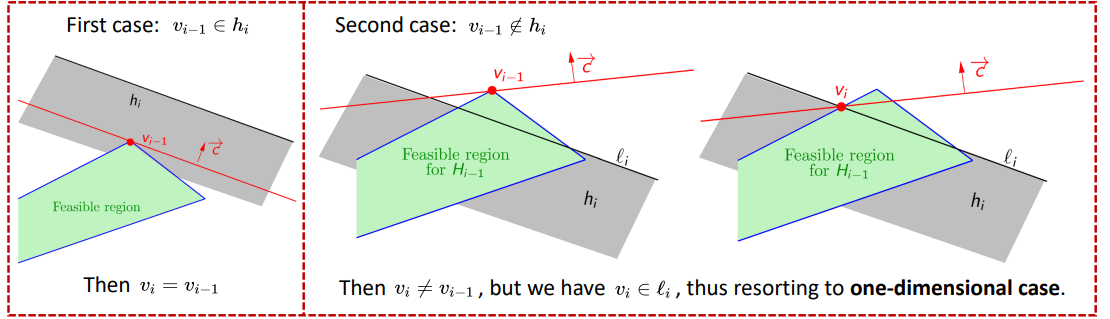
当新约束的半空间包含原可行域时，$v_{opt}$不变。

其伪代码如下：

低维二次规划（QP）

目标函数及约束（考虑严格凸低维QP问题）：

$$\begin{aligned}\min_{x\in\mathbb{R}^n}\frac{1}{2}x^\mathrm{T}M_{\mathcal{Q}}x+c_{\mathcal{Q}}^\mathrm{T}x\text{, s.t. }A_{\mathcal{Q}}x\le b_{\mathcal{Q}}\end{aligned}$$

因为是严格凸的，所以$M_{\mathcal{Q}}\succ0$，且是对称的所以可以进行分解：

$$M_{\mathcal{Q}}=L_{\mathcal{Q}}L_{\mathcal{Q}}^{\mathrm{T}}$$

我们将其构造成求最小范数问题：

$$\min_{y\in\mathbb{R}^n}\frac12y^\mathrm{T}y,\mathrm{~s.t.~}Ey\leq f$$

其中：

$$E=A_{\mathcal Q}L_{\mathcal Q}^{-\mathrm{T}},f=A_{\mathcal Q}\big(L_{\mathcal Q}L_{\mathcal Q}^{\mathrm{T}}\big)^{-1}c_{\mathcal Q}+b_{\mathcal Q}$$

是如何构造成上述形式呢？

$$y=L_{\mathcal Q}^{\mathrm T}x+L_{\mathcal Q}^{-1}c_{\mathcal Q}\quad\mathrm{or}\quad x=L_{\mathcal Q}^{-\mathrm T}y-\left(L_{\mathcal Q}L_{\mathcal Q}^{\mathrm T}\right)^{-1}c_{\mathcal Q}$$

即我们先求得最小范数问题的解$y^*$，再根据上式求得$x^*$。

如下图所示：

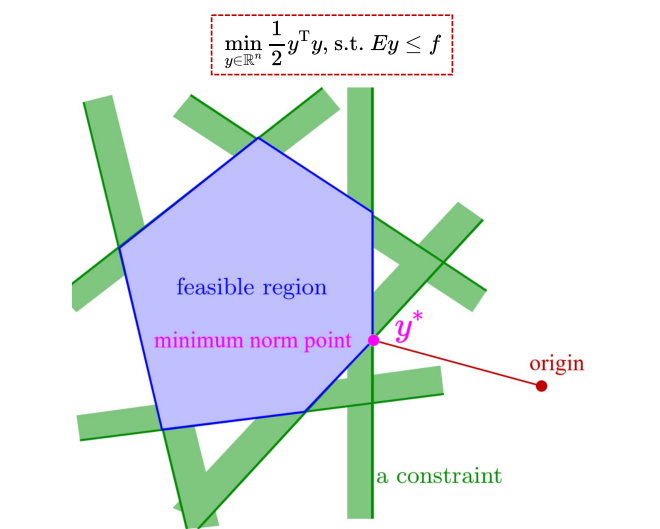
其伪代码为：

约束优化的三种序列无约束优化方法

外点罚函数法

参考链接：内点罚函数和外点罚函数的优缺点

简而言之，外点罚函数法是指对于可行域外的点，惩罚项为正，即对该点进行惩罚；对于可行域内的点，惩罚项为0，即不做任何惩罚。因此，该算法在迭代过程中点列一般处于可行域之外，惩罚项会促使无约束优化问题的解落在可行域内。罚函数一般由约束部分乘正系数组成，通过增大该系数，我们可以更严厉地惩罚违反约束的行为，从而迫使惩罚函数的最小值更接近约束问题的可行区域。

$L_2-Penalty\; Function: Equality\; Constrained\; Case$

只具有等式约束的规划问题：

$$\begin{array}{cc}\min_x&f(x)\\\mathrm{s.t.}&c_i(x)=0,\quad i\in\mathcal{E}\end{array}$$

该规划问题的惩罚函数为：

$$P_E(x,\sigma)=f(x)+\color{red}{\frac{1}{2}}\sigma\sum_{i\in\mathcal{E}}c_i^2(x)$$

红色部分是二次惩罚函数，其中$\sigma$是惩罚权重。

一般的，随着惩罚权重的增加，无约束的最小值接近受约束的最小值。

$$\lim_{\sigma\to+\infty}\operatorname{argmin}_{x}P_{E}(x,\sigma)=\operatorname{argmin}_{x}f(x),\text{s.t.}c_{i}(x)=0,i\in\mathcal{E}$$

$L_2-Penalty\; Function: Inequality\; Constrained\; Case$

对于不等式约束的规划问题：

$$\begin{array}{cc}\min&f(x)\\\mathrm{s.t.}&c_i(x)\leqslant0,\quad i\in\mathcal{I}\end{array}$$

其惩罚函数为：

$$P_I(x,\sigma)=f(x)+\color{red}{\frac{1}{2}}\sigma\sum_{i\in\mathcal{I}}\max[c_i(x),0]^2$$

同样的上述式子的红色部分是二次惩罚项，但是其二阶导数不是连续的。

随着惩罚权重的增加，无约束的最小值接近受约束的最小值。

$$\lim\limits_{\sigma\to+\infty}\operatorname{argmin}_{x}P_{I}(x,\sigma)=\operatorname{argmin}_{x}f(x),\text{s.t.}c_{i}(x)\leq0,i\in\mathcal{I}$$

优点：

• 将约束优化问题转化为无约束优化问题，当$c_i(x)$光滑时可以调用一般的无约束光滑优化问题算法求解;
• 二次罚函数形式简洁直观而在实际中广泛使用。

缺点：

• 需要$\sigma\rightarrow\infty $，此时海瑟矩阵条件数过大，对于无约束优化问题的数值方法拟牛顿法与共轭梯度法存在数值困难，且需要多次迭代求解子问题；
• 对于存在不等式约束的$P(x,\sigma)$可能不存在二次可微性质，光滑性降低;
• 不精确，与原问题最优解存在距离。

$L_1-Penalty\; Function: Exactness$

由于L2-罚函数法存在数值困难，并且与原问题的解存在误差，因此考虑精确罚函数法。精确罚函数是一种问题求解时不需要令罚因子趋于正无穷（或零）的罚函数。换句话说，若罚因子选取适当，对罚函数进行极小化得到的解恰好就是原问题的精确解。这个性质在设计算法时非常有用，使用精确罚函数的算法通常会有比较好的性质。由于L1-罚函数非光滑，因此无约束优化问题P的收敛速度无法保证，这实际上就相当于用牺牲收敛速度的方式来换取优化问题P的精确最优解。

一般的具有约束的优化问题同时包含等式约束和不等式约束：

$$\begin{array}{rl}\min&f(x)\\\mathrm{s.t.}&c_i(x)=0,&i\in\mathcal{E}\\&c_j(x)\leqslant0,&j\in\mathcal{I}\end{array}$$

其惩罚函数是：

$$P(x,\sigma)=f(x)+\color{red}{\sigma\sum_{i\in\mathcal{E}}|c_i(x)|+\sigma\sum_{j\in\mathcal{I}}\max[c_j(x),0]}$$

红色部分是L1惩罚函数，他的导数是不连续的。

有：

$$\exists M\in\mathbb{R}_{>0},\forall\sigma>M,\operatorname{argmin}_xP(x,\sigma)=\operatorname{argmin}_xf(x),\operatorname{s.t.}c_i(x)=0,i\in\mathcal{E},c_j(x)\leq0,j\in\mathcal{I}$$

内点罚函数法：障碍函数法

前面介绍的L1和L2罚函数均属于外点罚函数，即在求解过程中允许自变量$x$位于原问题可行域之外，当罚因子趋于无穷时，子问题最优解序列从可行域外部逼近最优解。自然地，如果我们想要使得子问题最优解序列从可行域内部逼近最优解，则需要构造内点罚函数。顾名思义，内点罚函数在迭代时始终要求自变量$x$不能违反约束，因此它主要用于不等式约束优化问题。

如下图所示，考虑含不等式约束的优化问题，为了使迭代点始终在可行域内，当迭代点趋于可行域边界时，我们需要罚函数趋于正无穷。常见的罚函数有三种：对数罚函数，逆罚函数和指数罚函数。对于原问题，它的最优解通常位于可行域边界，即$c_{i}\left(x\right)\leq0$中至少有一个取到等号，此时需要调整惩罚因子$\sigma$使其趋于0，这会减弱障碍罚函数在边界附近的惩罚效果。

不等式约束的规划问题：

$$\begin{array}{cc}\min&f(x)\\\mathrm{s.t.}&c_i(x)\leqslant0,\quad i\in\mathcal{I}\end{array}$$

三种障碍函数的式子为：

• 对数障碍函数：

  $$B_{\ln}(x,\sigma)=f(x)-\color{red}\sigma\sum_{i\in\mathcal{I}}\ln(-c_i(x))$$

• 逆障碍函数：

  $$B_{\mathrm{inv}}(x,\sigma)=f(x)+\color{red}\sigma\sum_{i\in\mathcal{I}}\text{inv}(-c_i(x)),\text{inv}(x):=1/x\text{if}x>0$$

• 指数障碍函数：

  $$B_\text{expi}(x,\sigma)=f(x)+\color{red}{\sigma\sum_{i\in\mathcal{I}}\text{expi}(-c_i(x))},\text{expi}(x):=e^{1/x}\text{if}x>0$$

通常地，随着权重的衰减，无约束的最小值接近受约束的最小值

$$\lim_{\sigma\to0^+}\operatorname{argmin}_xB(x,\sigma)=\operatorname{argmin}_xf(x),\mathrm{s.t.~}c_i(x)\leq0,i\in\mathcal{I}$$

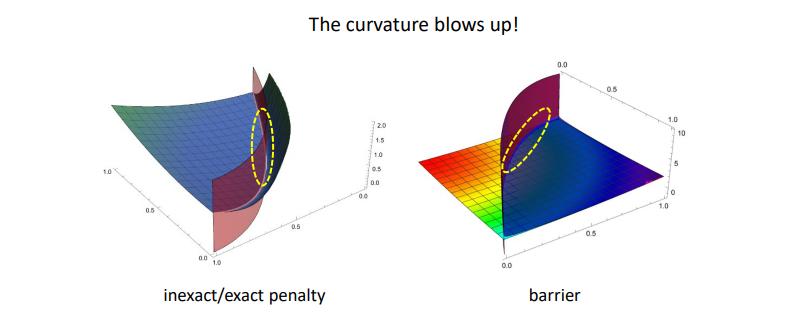
总结

如下图所示，无论是外点惩罚法或者是内点惩罚法，随着权重趋于无穷或者趋于0都会导致函数变得不光滑，海森矩阵条件数趋于无穷，因此使用数值方法（拟牛顿法等）求解会越来越困难。

等式约束优化问题的拉格朗日松弛法

参考链接：

“拉格朗日对偶问题”如何直观理解？

【数学】拉格朗日对偶，从0到完全理解_拉格朗日法对偶格式

等式约束凸优化问题：

$$\begin{array}{ll}\min_x&f(x)\\\mathrm{s.t.}&Ax=b\end{array}$$

拉格朗日函数：

$$\mathcal{L}(x,\lambda):=f(x)+\langle\lambda,Ax-b\rangle=f(x)+\lambda^{T}(Ax-b)$$

显然有：

$$\left.\max_{\lambda}f(x)+\langle\lambda,Ax-b\rangle=\left\{\begin{matrix}f(x),Ax-b=0\\\infty,\mathrm{~otherwise}\end{matrix}\right.\right.$$

因此优化问题等价于，

$$\min_xf(x),\text{ s.t. }Ax=b\quad\longleftrightarrow\quad\min_x\max_\lambda\mathcal{L}(x,\lambda)$$

约束优化问题的最优解正是拉格朗日的鞍点。

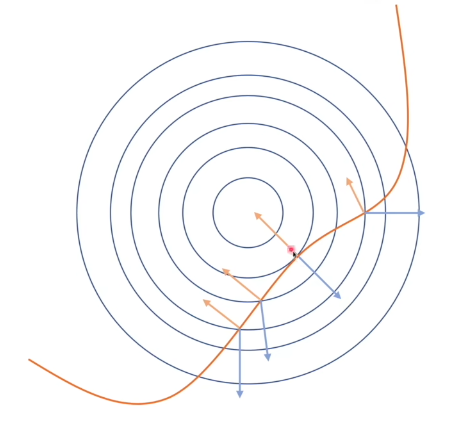
Uzawa’s Method

综上分析，Uzawa’s Method迭代过程分为两个步骤

$$\left.\left\{\begin{array}{l}x^{k+1}=\operatorname{argmin}\mathcal{L}\left(x,\lambda^k\right)\\\lambda^{k+1}=\lambda^k+\alpha\left(Ax^{k+1}-b\right)\end{array}\right.\right.$$

1. 给定$\lambda^{k}$，求解$\operatorname*{min}_{x}\mathcal{L}(x,\lambda^{k})$无约束优化问题，求解得到$x^{k+1}$
2. 更新$\lambda$，$L(x^{k+1},\lambda)$关于$\lambda$的梯度为$\left.\frac{\partial L}{\partial\lambda}\right|_{x+1}=Ax^{k+1}-b$，若要求解$\operatorname*{max}_{\lambda}\mathcal{L}(x^{k+1},\lambda)$，则沿着梯度上升方向进入步长迭代，即$\lambda^{k+1}=\lambda^k+\alpha\left(Ax^{k+1}-b\right)$，$\sigma$为迭代步长。

该方法的前提就是原函数连续凸，$\mathcal{L}(x,\lambda)$关于$x$严格凸，则$\operatorname*{min}_{x}\mathcal{L}(x,\lambda^{k})$只存在一个最优解，可求出唯一$x^{k+1}$进而更新$\lambda^{k+1}$，否则$x^{k+1}$会存在多个，不知道选择哪个去更新$\lambda$。因此缺点很明显，该方法要求原函数必须为连续凸函数，梯度上升步长需要调整且收敛速率不能保证。

• 原始优化问题应该是凸的。
• 关于原始变量的拉格朗日函数应该是严格凸的。
• 对偶上升步长需要调整。
• 收敛速度不理想。

一般约束优化的方法

KKT条件

参考链接：Karush-Kuhn-Tucker (KKT)条件

Karush-Kuhn-Tucker (KKT)条件是非线性规划(nonlinear programming)最佳解的必要条件。KKT条件将Lagrange乘数法(Lagrange multipliers)所处理涉及等式的约束优化问题推广至不等式。在实际应用上，KKT条件(方程组)一般不存在代数解，许多优化算法可供数值计算选用。

一般的约束优化问题

$$\begin{array}{ll}\min_x&f(x)\\\mathrm{s.t.}&h_i(x)\leq0,i=1,\ldots,m\\&\ell_j(x)=0,j=1,\ldots,r\end{array}$$

如果上述优化问题没有退化即不等式约束起了作用（这句话具体理解可以看参考链接），它的最优解满足：

• stationarity

  $$0\in\partial_x[f(x)+\sum_{i=1}^mu_ih_i(x)+\sum_{j=1}^rv_j\ell_j(x)]$$

• complementary slackness

  $$u_i\cdot h_i(x)=0,i=1,\ldots,m$$

• primal feasibility

  $$h_i(x)\leq0,\ell_j(x)=0,i=1,\ldots,m,j=1,\ldots,r$$

• dual feasibility

  $$u_{i}\geq0,i=1,\ldots,m$$

Powell-Hestense-Rockafellar Augmented-Lagrangian-Method（PHR-ALM）

参考链接：

约束优化：PHR-ALM 增广拉格朗日函数法

“拉格朗日对偶问题”如何直观理解？

对于等式约束优化问题：

$$\begin{aligned}\min_{x\in\mathbb{R}^n}&f(x)\\\text{s.t.}&h(x)=0\end{aligned}$$

Uzawa的方法是对偶函数进行双梯度上升：

$$d(\lambda):=\min_xf(x)+\lambda^\text{T}h(x)$$

如果关于x的拉格朗日函数不是严格凸的，对偶函数就是非光滑的。那么其梯度就可能不存在，这是这种方法就会出现问题。

已知$\left.\operatorname*{max}_{\lambda}f(x)+\lambda^{\mathrm{T}}h(x)=\left\{\begin{array}{l}{f(x),h(x)=0}\\{\infty,\mathrm{~otherwise}}\end{array}\right.\right.$是一个不连续函数，如何处理这个不连续的函数，一个非常直观的方法就是将该问题近似成一个连续问题，这是PHR的基本思想。如何近似呢？增加一项$\frac{1}{2\rho}\|\lambda-\bar{\lambda}\|^2$，用来近似平滑原来不连续的函数$\max_{\lambda}f(x)+\lambda^{\mathrm{T}}h(x)$，其中$\rho>0$用来惩罚$\lambda$与先验值$\bar{\lambda}$之间的偏差。

$$\min_x\max_\lambda f(x)+\lambda^\text{T}h(x)-\color{red}\frac{1}{2\rho}\|\lambda-\bar{\lambda}\|^2$$

这样一来，函数被近似成一个光滑函数，同时$f(x)+\lambda^{\mathrm{T}}h(x)$是关于$\lambda$的线性函数，既是凸函数又是凹函数，而且$-\frac1{2\rho}\|\lambda-\bar{\lambda}\|^2$是关于$\lambda$的严格凹函数，因此整个函数仍为严格凹，对于严格凹问题$\operatorname*{max}_{\lambda}f(x)+\lambda^{\mathrm{T}}h(x)-\frac{1}{2\rho}\|\lambda-\bar{\lambda}\|^{2}$有唯一最优解$\lambda^{*}$满足：

$$\frac{\partial\left\{f(x)+\lambda^\top h(x)-\frac1{2\rho}\left\|\lambda-\bar\lambda\right\|^2\right\}}{\partial\lambda}=h(x)-\frac1\rho\left(\lambda-\bar{\lambda}\right)=0$$

可解得

$$\lambda^*(\bar{\lambda})=\bar{\lambda}+\rho h(x)$$

带入到原式中：

$$\begin{aligned} &\min_x\max_\lambda f(x)+\lambda^\mathrm{T}h(x)-\frac1{2\rho}\|\lambda-\bar{\lambda}\|^2 \\ &=\min_x\left.f(x)+\lambda^*(\bar{\lambda})^{\mathrm{T}}h(x)-\frac1{2\rho}\left.\right\Vert\lambda^*(\bar{\lambda})-\bar{\lambda}\Vert^2\right. \\ &=\min_xf(x)+(\bar{\lambda}+\rho h(x))^\text{T}h(x)-\frac\rho2\|h(x)\|^2 \\ &=\min_xf(x)+\bar{\lambda}^\mathrm{T}h(x)+\frac\rho2\|h(x)\|^2 \end{aligned}$$

上述都是近似的过程，但是我们如何确保近似的精度呢？

1. 减少近似权重，使$\frac1\rho\to0$或$\rho\to+\infty $
2. 更新先验值$\bar{\lambda}\leftarrow\lambda^{*}(\bar{\lambda})$

对于等式约束的PHR更新方法：

$$\begin{aligned} &x\leftarrow\arg\min_{x}f(x)+\bar{\lambda}^{\mathrm{T}}h(x)+\frac{\rho}{2}\|h(x)\|^{2} \\ &\bar{\lambda}\leftarrow\bar{\lambda}+\rho h(x) \end{aligned}$$

拉格朗日函数变为增广拉格朗日函数：

$$\min_x\max_\lambda f(x)+\frac{\rho}{2}\|h(x)\|^2+\lambda^\text{T}h(x)$$

明显地，相应的原始问题变为

$$\begin{aligned}\min_{x\in\mathbb{R}^n}f(x)+\frac{\rho}{2}\|h(x)\|^2\\\text{s.t.}h(x)=0\end{aligned}$$

此时得到一个与原问题近似的无约束最优化问题，通过在原拉格朗日函数的基础之上增加一个增广项获得一个增广拉格朗日函数，来得到近似光滑且容易解的优化问题。

对于原本非凸等式约束优化问题：

$$\begin{aligned}\min_{x\in\mathbb{R}^n}&f(x)\\\text{s.t.}&h(x)=0\end{aligned}$$

其PHR增广拉格朗日函数的更常用等效形式为：

$$\mathcal{L}_{\rho}(x,\lambda):=f(x)+\frac{\rho}{2}\Big\Vert h(x)+\frac{\lambda}{\rho}\Big\Vert^{2}$$

KKT解析可以通过以下方式解决：

$$\begin{cases}x^{k+1}=\operatorname{argmin}_x\mathcal{L}_{\rho^k}(x,\lambda^k)\\\lambda^{k+1}=\lambda^k+\rho^kh\big(x^{k+1}\big)\\\rho^{k+1}=\min[(1+\gamma)\rho^k,\beta]\end{cases}$$

• $p^k$迭代过程不是下降的，$\gamma\geq0,\beta>0,\rho^{0}>0$
• 不需要每次都求解很精确的$x^k$，因为外循环会不断的细化$\lambda^{k}$和$x^k$

对于不等式约束非凸优化问题：

对于不等式约束的非凸问题，核心思想是通过引入松弛变量$s$，将不等式约束转化为等式约束，然后再写成增广拉格朗日函数形式。如下图所示，引入松弛变量$s$，原问题维度从n维上升到n+m维。原问题为：

$$\begin{array}{rl}\min_{x\in\mathbb{R}^n}&f(x)\\\mathrm{s.t.}&g(x)\leq0\end{array}$$

引入松弛变量后变为等式约束的非凸优化问题：

$$\begin{aligned}&\min_{x\in\mathbb{R}^n,s\in\mathbb{R}^m}f(x)\\&\mathrm{s.t.}\quad g(x)+[s]^2=0\end{aligned}$$

将转化后的问题写成增广拉格朗日函数形式：

$$\min_{x\in\mathbb{R}^n,s\in\mathbb{R}^m}f(x)+\frac\rho2\left\|g(x)+[s]^2+\frac\lambda\rho\right\|^2=\min_{x\in\mathbb{R}^n}\min_{s\in\mathbb{R}^m}f(x)+\frac\rho2\left\|g(x)+[s]^2+\frac\lambda\rho\right\|^2=\min_{x\in\mathbb{R}^n}f(x)+\color{red}{\frac\rho2}\left\|\max\left[g(x)+\frac\lambda\rho,0\right]\right\|^2$$

为了与等式约束拉格朗日乘子区别开我们将$\lambda$写成$\mu$

$$\mathcal{L}_{\rho}(x,\mu):=f(x)+\frac{\rho}{2}\Big\Vert\max\big[g(x)+\frac{\mu}{\rho},0\big]\Big\|^{2}$$

其中$\rho>0,\mu\succeq0$。PHR-ALM只是重复下降+对偶函数上升迭代。

$$\begin{cases}x\leftarrow\operatorname{argmin}_x\mathcal{L}_\rho(x,\lambda,\mu)\\\lambda\leftarrow\lambda+\rho h(x)\\\mu\leftarrow\max[\mu+\rho g(x),0]\\\rho\leftarrow\min[(1+\gamma)\rho,\beta]\end{cases}$$

• 如何选择参数

  $$\rho_{\mathrm{ini}}=1,\lambda_{\mathrm{ini}}=\mu_{\mathrm{ini}}=0,\gamma=1,\beta=10^3$$

• 内层循环迭代停止条件，内层循环就是解无约束优化问题

  $$\left.\|\nabla_x\mathcal{L}_\rho(x,\lambda,\mu)\|_\infty<\xi^k\min\left[1,\max\left[\|h(x)\|_\infty,\right\|\max\left[g(x),-\frac\mu\rho\right]\right\|_\infty\right]\text{with positive }\xi^k\text{ converging to }0$$

• 外层迭代停止条件，即度量KKT条件的残差

  $$\max\left[\left\|h(x)\right\|_{\infty},\left\|\max\left[g(x),-\frac{\mu}{\rho}\right]\right\|_{\infty}\right]<\epsilon_{\mathrm{cons}},\left\|\nabla_{x}{\mathcal L}_{\rho}(x,\lambda,\mu)\right\|_{\infty}<\epsilon_{\mathrm{prec}}$$

应用

参考链接：约束优化的应用：控制分配问题、碰撞距离计算、非线性MPC

控制分配问题、碰撞距离计算、非线性模型预测控制

作业

作业一：严格凸的等式约束QP的KKT推导和求解

问题如下：

$$\begin{aligned}\min_{x\in\mathbb{R}^n}\frac{1}{2}x^\top Qx+c^\top x\\s.t.Ax=b\end{aligned}$$

其中$Q$是对称正定矩阵（spd）。

根据课程所学，它的最优解满足：

• stationarity

  $$0\in\partial_x[f(x)+\sum_{i=1}^mu_ih_i(x)+\sum_{j=1}^rv_j\ell_j(x)]$$

  即：

  $$\partial_x[\frac{1}{2}x^\top Qx+c^\top x+v(Ax-b)]=0$$

  可得：

  $$Qx+c^\top+vA=0$$

• complementary slackness

  无

• primal feasibility

  $$Ax-b=0$$

• dual feaesibility

  无

综上，假设最优解为$x^{*}$，$v^{*}$其满足

$$\begin{cases}Qx^*+c+A^Tv^*=0\\Ax^*=b\end{cases}$$

有

$$\begin{bmatrix}Q&A^T\\A&0\end{bmatrix}\begin{bmatrix}x^*\\v^*\end{bmatrix}=\begin{bmatrix}-c\\b\end{bmatrix}$$

下面我们还需证明$\begin{bmatrix}Q&A^T\\A&0\end{bmatrix}$可逆

我们构造下面这个式子

$$\begin{bmatrix}I&0\\-AQ^{-1}&I\end{bmatrix}\begin{bmatrix}Q&A^T\\A&0\end{bmatrix}\begin{bmatrix}I&-Q^{-1}A^T\\0&I\end{bmatrix}=\begin{bmatrix}Q&0\\0&-AQ^{-1}A^T\end{bmatrix}$$

因为$Q$是对称正定(SPD)的，所以$-AQ^{-1}A^T$也是对称正定(SPD)，所以$\begin{bmatrix}Q&0\\0&-AQ^{-1}A^T\end{bmatrix}$是可逆的，即$\begin{bmatrix}Q&A^T\\A&0\end{bmatrix}$可逆。

则此QP问题的解为：

$$\begin{bmatrix}x^*\\y^*\end{bmatrix}=\begin{bmatrix}Q&A^T\\A&0\end{bmatrix}^1\!\begin{bmatrix}-c\\b\end{bmatrix}$$

作业二：低维严格凸QP线性时间复杂度算法的补全

根据课程算法：

根据伪代码补全即可（详细代码见文件）

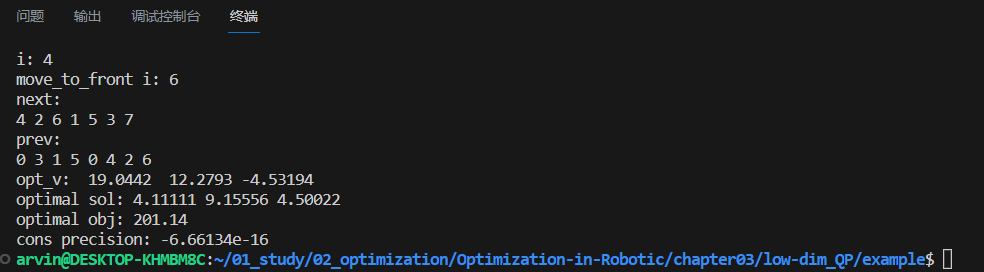
编译然后运行可执行文件结果如下：

作业三：用PHR-ALM方法求解NMPC

分析

根据课程MPC问题可以表示成：

$$\begin{aligned}\min_{u_{0:N}}J(s_1(u_{0:N}),\ldots,s_N(u_{0:N}),u_{0:N})\\\mathrm{s.t.~}G(s_k(u_{0:N}),u_k)\leq0,\mathrm{~}\forall i\in\{0,\ldots,N\}\end{aligned}$$

其中

$$J(s_1,\ldots,s_N,u_0,\ldots,u_N):=\sum_{k=1}^N[(x_k-x_k^\mathrm{ref})^2+(y_k-y_k^\mathrm{ref})^2+w_v(a_k-a_{k-1})^2+w_\delta(\delta_k-\delta_{k-1})^2]$$

$$F({s_k},{u_k})={s_{k+1}},\mathrm{~}\forall\mathrm{~}i\in\{0,\ldots,N\}\quad\boldsymbol{\longleftrightarrow}\quad\boldsymbol{s_k}({u_{0:N}}),\mathrm{~}\forall\mathrm{~}i\in\{1,\ldots,N\}$$

$$\begin{aligned} &\mathrm{~}\forall\mathrm{~}k\in\{0,\ldots,N\} \\ &a_{\mathrm{min}}\leq a_{k}\leq a_{\mathrm{max}} \\ &\delta_{\mathrm{min}}\leq\delta_{k}\leq\delta_{\mathrm{max}}& G(s_k,u_k)\leq0 \\ &v_{\mathrm{min}}\leq v_{k}\leq v_{\mathrm{max}} \end{aligned}$$

加入松弛变量，我们可以得到：

$$G(s_k(u_{0:N}),u_k)+[s]^2=0$$

所以拉格朗日函数为：

$$L(u_{0.N},\mu):=J(s_{1}(u_{0.N}),...,s_{N}(u_{0.N}),u_{0.N})+\frac{\rho}{2}\biggr\Vert\max(\begin{array}{c}G(s_{k}(u_{0.N}),u_{k})+\frac{\mu}{\rho},0\end{array}\biggr\Vert^{2}$$

然后进行迭代：

$$\begin{cases}u_{0:N}\gets\arg\min L_p(u_{0:N},\mu)\\\mu\gets\max[\mu+\rho G(s_k(u_{0:N}),u_k),0]\\\rho\gets\min[(1+\gamma)\rho,\beta]\end{cases}$$

运行

1. 根据说明安装osqp

2. 创建工作空间，将src文件夹复制进去。

3. 编译
   cd catkin_ws

   catkin_make

4. 执行launch文件
   roslaunch mpc_car simulation.launch

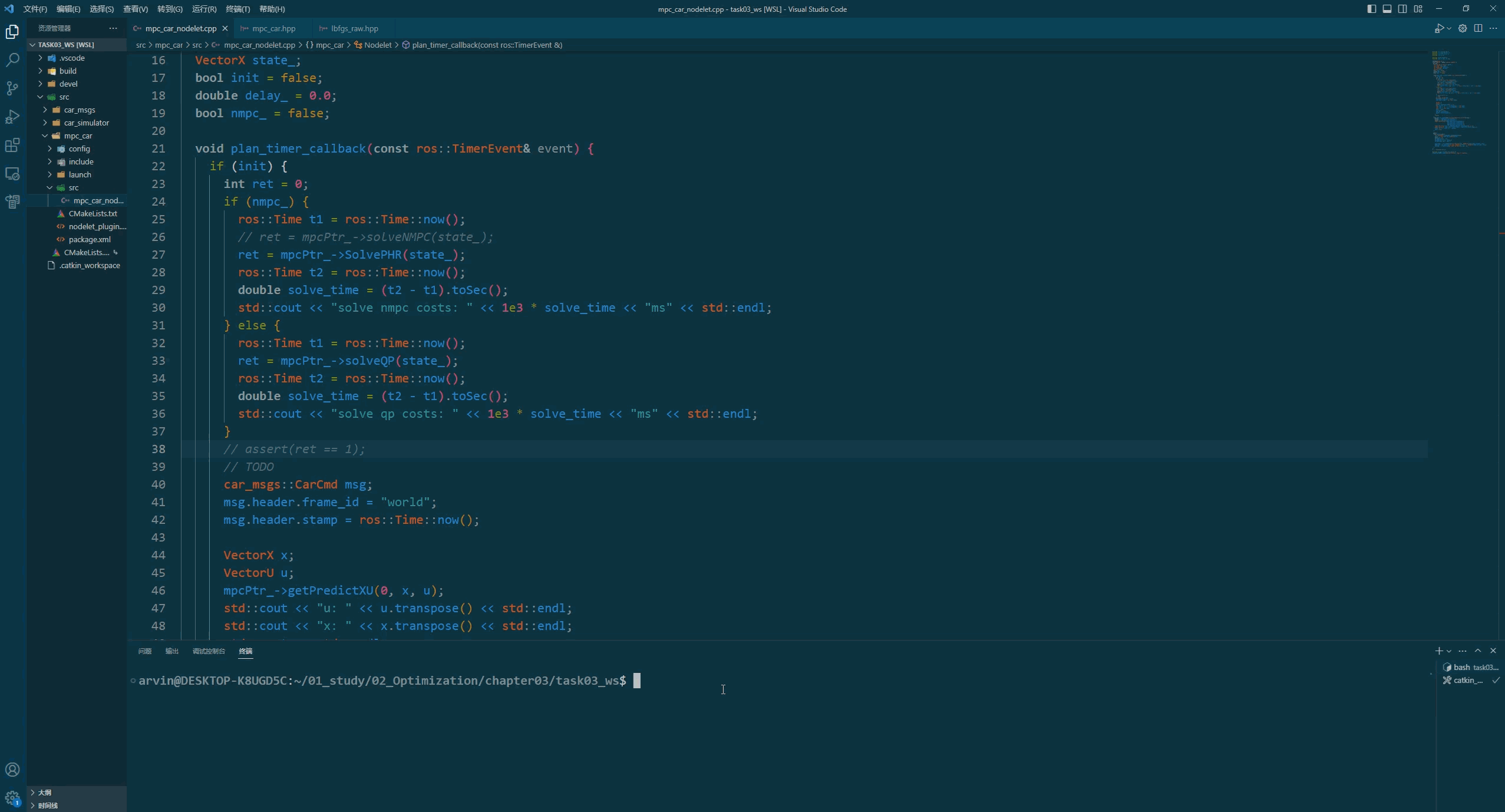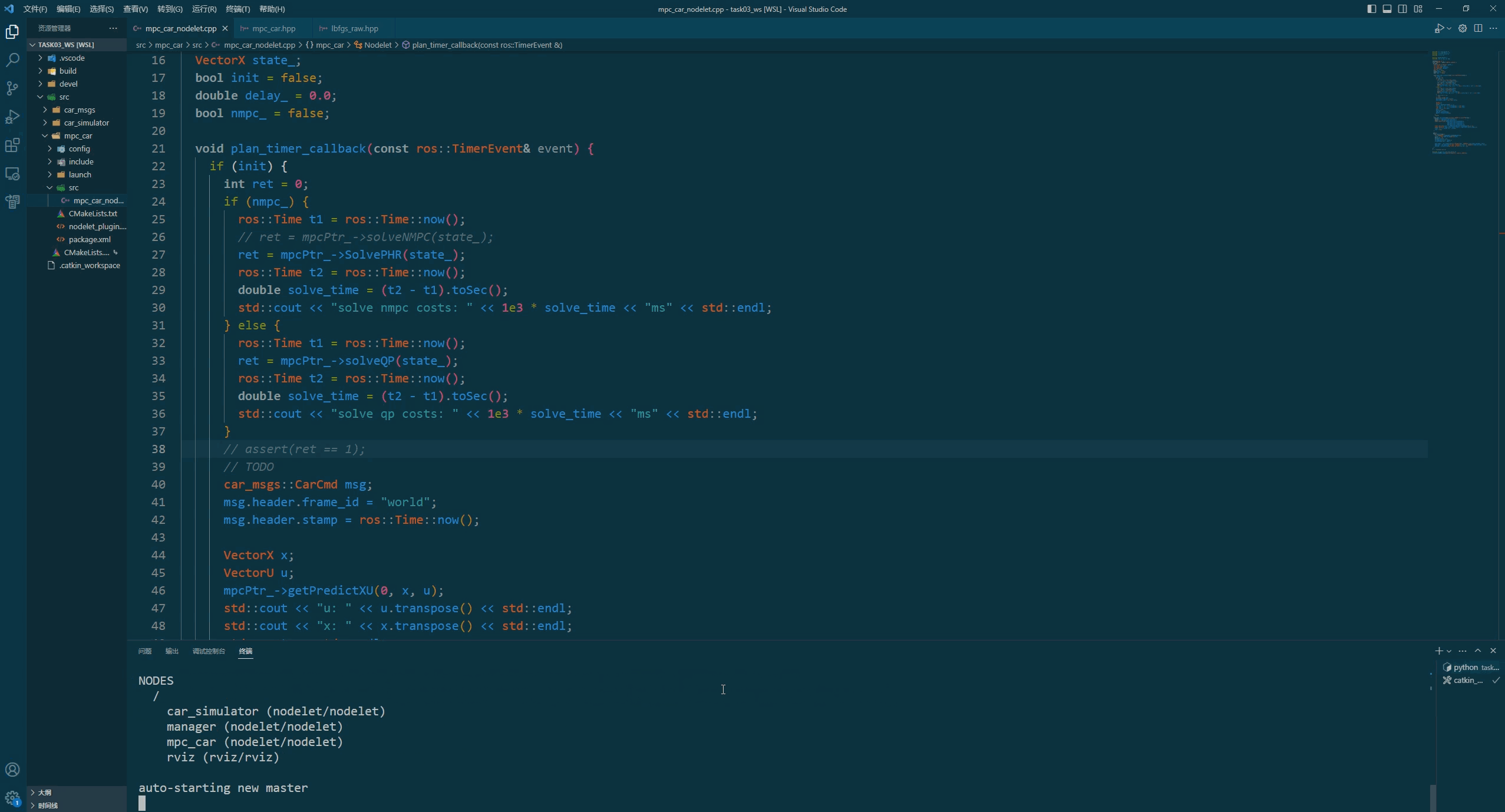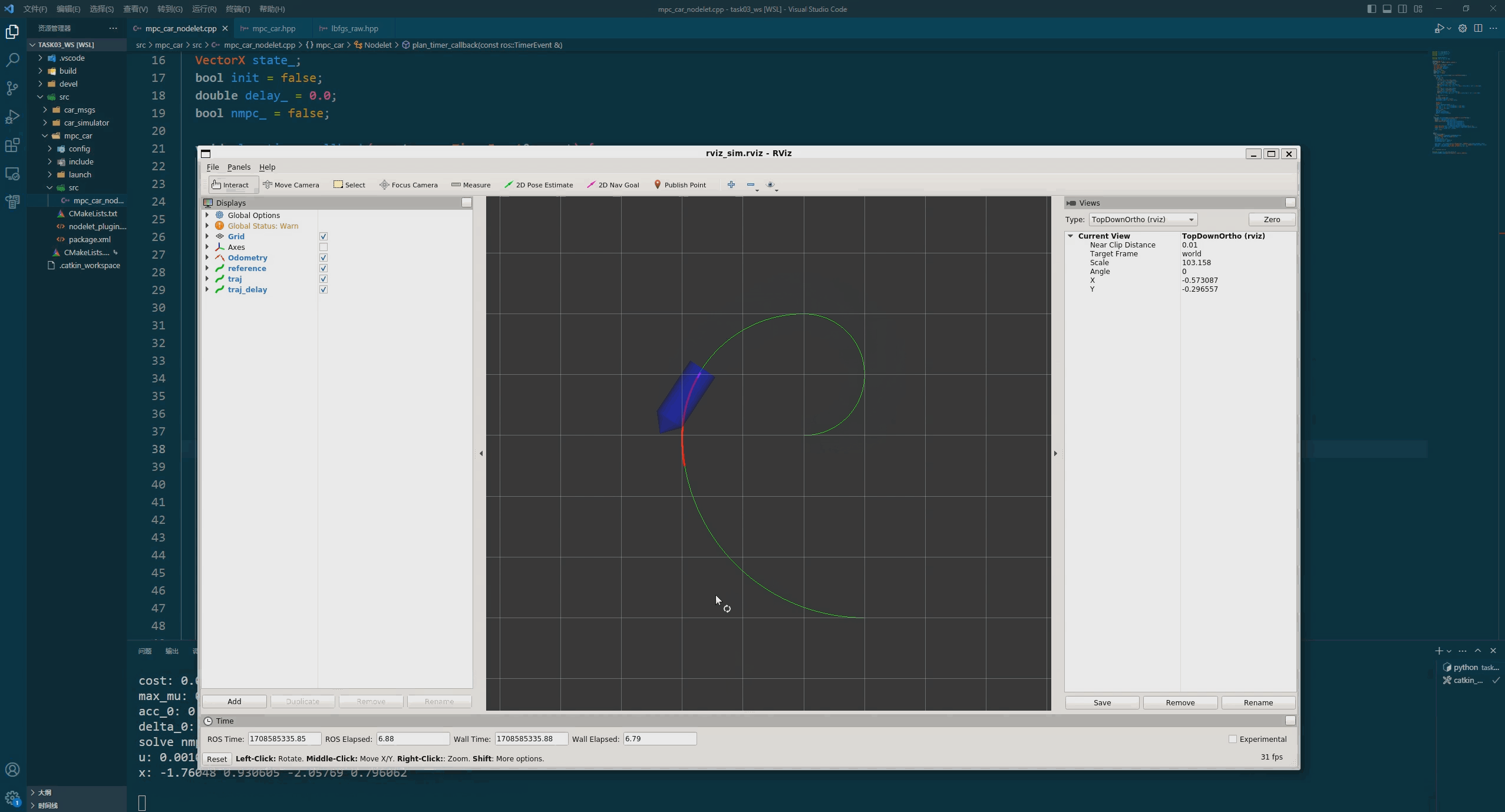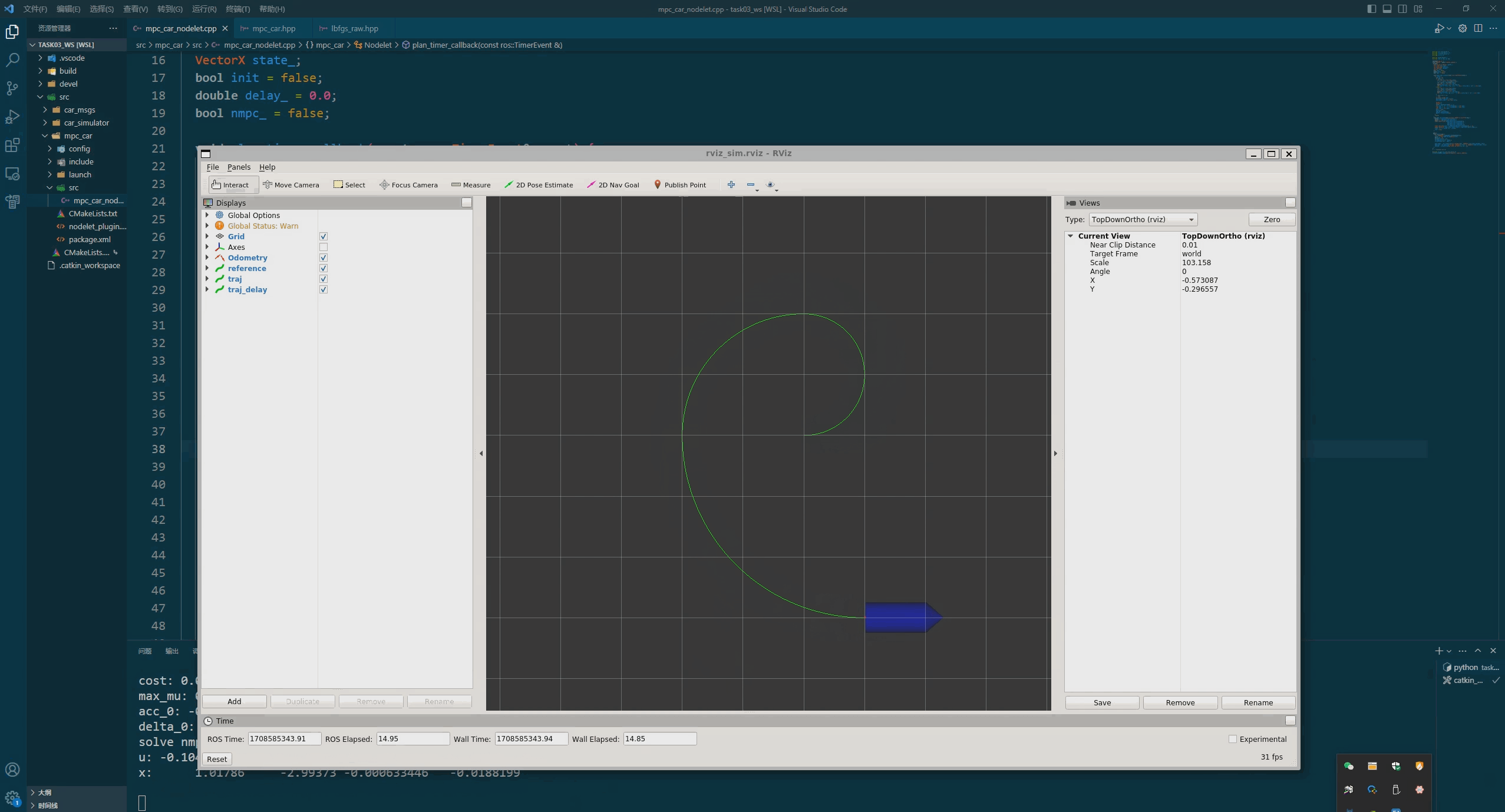
结果

如下图所示：