RL in Constraint Manifold

文档维护：Arvin

网页部署：Arvin

▶

Abstract

由于许多实际问题，包括安全、机械约束和磨损，机器人技术中的强化学习极具挑战性。

通常，这些问题在机器学习文献中没有被考虑。在现实世界中应用强化学习的一个关键问题是安全探索，这需要在整个学习过程中满足物理和安全约束。为了在这样一个安全关键的环境中进行探索，利用机器人模型和约束等已知信息有助于提供更强大的安全保证。利用这些知识，我们提出了一种新的方法，在满足学习过程中的约束的情况下，有效地学习仿真中的机器人任务。

Introduction

深度强化学习虽然在一些问题上表现的很好，但是在现实世界中使用强化学习还是一项具有挑战性的任务，因为典型的强化学习算法，通过不断试错来最大化累计奖励，并没有考虑在探索过程中对约束的满足，而在实际世界中智能体在探索过程中要受到许多约束。

文章提出了一种新方法，在流形空间的切平面上执行动作（Acting on the Tangent Space of the Constraint Manifold, ATACOM）。该方法将约束强化学习问题转化成无约束强化学习问题。

ATACOM的优势可以概括如下:

• 可以处理等式约束和不等式约束。在整个学习过程中，每个时间步的都在约束范围内。
• 不需要初始可行策略，智能体可以从零开始学习。
• 不需要手动将系统移回安全区域的安全备份策略。
• 可以应用于任何无模型RL算法，使用确定性和随机策略。
• 可以将探索的重点放在低维流形上，而不是在原来的行动空间中探索等式约束问题。
• 由于不等式约束约束在更小的可行状态-动作空间内，学习性能更好。

缺点:

• 可微的约束函数。
• 机器人足够精确的可逆动力学模型或性能良好的跟踪控制器。

Learning on the Constraint Manifold

参数：
$q$：状态变量

$a=\boldsymbol{\Lambda}(\dot{\boldsymbol{q}})$：速度

$a=\boldsymbol\Lambda({\ddot{\boldsymbol{q}}})$：加速度

其中，在机器人的角度看，这个$a$可以是施加在每个关节上的扭矩，$\Lambda $是逆动力学模型。

带约束的马尔可夫过程CMDP:
CMDP是一个元组$(\mathcal{S},\mathcal{A},P,R,\gamma,\mathcal{C})$，其中

• $\mathcal{S}$：状态空间
• $\mathcal{A}$：动作空间
• $P$：$\mathcal{S}\times\mathcal{A}\times\mathcal{S}\rightarrow[0,1]$，转移核，类似于状态转移概率矩阵？
• $R$：奖励
• $\gamma$：折扣因子
• $\mathcal{C}$：$\{c_{i}:\mathcal{S}\to\mathbb{R}|i\in1,...,k\}$，当前状态约束函数的集合

假设：
本文将状态变量$s\in\mathcal{S}$分解为直接可控状态$q\in\mathcal{Q}$和不可控状态$x\in\mathcal{X}$，即$\boldsymbol{s}=\left[\begin{array}{ll}\boldsymbol{q} & \boldsymbol{x}\end{array}\right]^{\top}$。并作出如下假设：

• 假设约束$c(\boldsymbol{q})\leq 0$是已知的，并且完全依赖于可控状态
• 假设动作$a$可以根据可控状态的$i$阶时间导数确定，即$\boldsymbol{a}=\boldsymbol{\Lambda}(\boldsymbol{q}^{(i)}), i \in \{1,2,...\}$

约束强化学习问题的一般形式可以表示为：

$$\max_{\boldsymbol{\theta}}\mathbb{E}_{\boldsymbol{s}_t,\boldsymbol{a}_t}\left[\sum_{t=0}^T\gamma^tr(\boldsymbol{s}_t,\boldsymbol{a}_t)\right],\quad\text{s.t.}\quad\boldsymbol{c}(\boldsymbol{q}_t)\leq\boldsymbol{0}$$

State Constraints

状态约束定义为：

$$f(\boldsymbol{q})=\boldsymbol{0},\quad\boldsymbol{g}(\boldsymbol{q})\leq\boldsymbol{0} \tag{1}$$

这里，$f:\mathbb{R}^Q\to\mathbb{R}^F,g:\mathbb{R}^Q\to\mathbb{R}^G$是等式约束$F$和不等式约束$G$的连续二阶可导$C^2$映射，并且$F<Q$，即等式约束的数量F少于Q，也就是说等式约束的个数比问题中自变量个数要少。并且加入松弛变量$\mu\in\mathbb{R}^{G}$，将上式转化为等式约束：

$$c(\boldsymbol{q},\boldsymbol{\mu})=\begin{bmatrix}f(\boldsymbol{q})&\boldsymbol{g}(\boldsymbol{q})+\frac12\boldsymbol{\mu}^2\end{bmatrix}^\mathsf{T}=\mathbf{0} \tag{2}$$

此约束集合是嵌入在$(Q+G)$维空间中的$(F+G)$维流形。

计算其时间导数：

$$\dot{\boldsymbol{c}}(\boldsymbol{q},\boldsymbol{\mu},\dot{\boldsymbol{q}},\dot{\boldsymbol{\mu}})=\begin{bmatrix}\boldsymbol{J}_f(\boldsymbol{q})&0\\\boldsymbol{J}_g(\boldsymbol{q})&\operatorname{diag}(\boldsymbol{\mu})\end{bmatrix}\begin{bmatrix}\dot{\boldsymbol{q}}\\\dot{\boldsymbol{\mu}}\end{bmatrix}=\boldsymbol{J}_c(\boldsymbol{q},\boldsymbol{\mu})\begin{bmatrix}\dot{\boldsymbol{q}}\\\dot{\boldsymbol{\mu}}\end{bmatrix} \tag{3}$$

$f(\boldsymbol{q})$和$f(\boldsymbol{q})$的雅可比矩阵$J_f\in\mathbb{R}^{F\times Q}$和$J_g\in\mathbb{R}^{G\times Q}$。将两个雅可比矩阵组合成完全约束集的雅可比矩阵$\boldsymbol{J}_{c}(\boldsymbol{q},\boldsymbol{\mu})\in\mathbb{R}^{(F+G)\times(Q+G)}$。

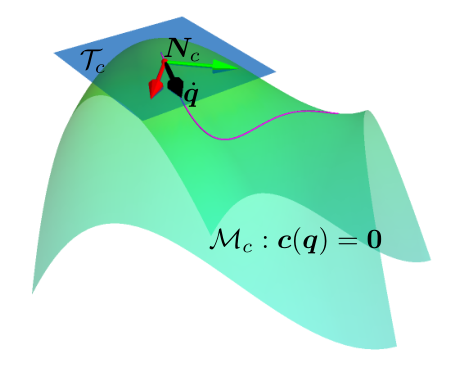
我们可以通过 SVD 分解或 QR 分解得到零空间矩阵$\boldsymbol{N}_{c}(\boldsymbol{q},\boldsymbol{\mu})=\mathrm{Null}[\boldsymbol{J}_{c}(\boldsymbol{q},\boldsymbol{\mu})]\in\mathbb{R}^{(Q+G)\times(Q-F)}$，使得$\boldsymbol{J}_{c}(\boldsymbol{q},\boldsymbol{\mu})\boldsymbol{N}_{c}(\boldsymbol{q},\boldsymbol{\mu})=\boldsymbol{0}$。正交矩阵$\boldsymbol{N}_{c}(\boldsymbol{q},\boldsymbol{\mu})$的每一列表示$\boldsymbol{J}_{c}(\boldsymbol{q},\boldsymbol{\mu})$的零空间的一个基向量。这些零空间基也可以看作约束流形的切空间基，如图1所示。我们可以用坐标$\alpha$来构造约束流形的切空间速度。

$$\begin{bmatrix}\dot{\boldsymbol{q}}\tau\\\dot{\boldsymbol{\mu}}\tau\end{bmatrix}=N_c(\boldsymbol{q},\boldsymbol{\mu})\boldsymbol{\alpha} \tag{4}$$

将公式（3）中的$[\dot{q}\quad\dot{\mu}]^{\mathsf{T}}$替换成（4）中的$[\dot{q}_{\mathcal{T}}\quad\dot{\mu}_{\mathcal{T}}]^{\mathsf{T}}$，则有

$$\dot{c}(\boldsymbol{q},\boldsymbol{\mu},\dot{\boldsymbol{q}},\dot{\boldsymbol{\mu}})=\boldsymbol{J}_c(\boldsymbol{q},\boldsymbol{\mu})\boldsymbol{N}_c(\boldsymbol{q},\boldsymbol{\mu})\boldsymbol{\alpha}=\boldsymbol{0} \tag{5}$$

方程（5）表明，无论$\alpha$的选择如何，约束都不会改变。基于这一概念，ATACOM方法可以概括为:从可行点出发$(\boldsymbol{q}(0),\boldsymbol{\mu}(0))\in\{(\boldsymbol{q},\boldsymbol{\mu})|\boldsymbol{c}(\boldsymbol{q},\boldsymbol{\mu})=\boldsymbol{0}\}$,我们选择切线空间速度$[\dot{\boldsymbol{q}}_{\mathcal{T}}(t),\dot{\boldsymbol{\mu}}_{\mathcal{T}}(t)]^{\mathsf{T}}={\boldsymbol{N}}_{c}(\boldsymbol{q}(t),\boldsymbol{\mu}(t))\boldsymbol{\alpha}(t)$和相应的行动$\boldsymbol{a}(t)=\boldsymbol{\Lambda}(\dot{\boldsymbol{q}}_{\mathcal{T}}(t))$。从而将约束RL问题转化为无约束RL问题。得到的轨迹$q(t)$满足约束条件$\boldsymbol{c}(\boldsymbol{q}(t),\boldsymbol{\mu}(t))=\mathbf{0}$。

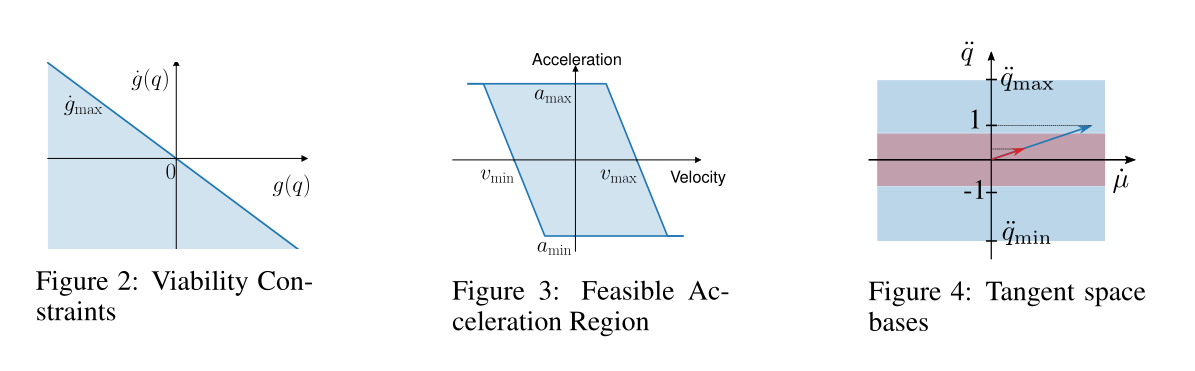
Viability Constraints

对于物理系统，通常需要一个连续的速度命令。然而，直接采样速度 $\dot q$ 并不能保证这种连续性。一个简单的解决方案是采样加速度，对系统施加力或通过积分确定速度。此外，在考虑不等式约束时，也希望当 $g(q)=0$ 时，$\dot g(q, \dot q) \le 0$，以避免过冲。

我们将原始状态约束(1)转换为受线性可行性条件启发的可行性约束：

$$\begin{aligned} \boldsymbol{f}(\boldsymbol{q})+\boldsymbol{K}_{f} \dot{\boldsymbol{f}}(\boldsymbol{q}, \dot{\boldsymbol{q}}) & =\boldsymbol{f}(\boldsymbol{q})+\boldsymbol{K}_{f} \boldsymbol{J}_{f}(\boldsymbol{q}) \dot{\boldsymbol{q}}=\mathbf{0} \\ \boldsymbol{g}(\boldsymbol{q})+\boldsymbol{K}_{g} \dot{\boldsymbol{g}}(\boldsymbol{q}, \dot{\boldsymbol{q}}) & =\boldsymbol{g}(\boldsymbol{q})+\boldsymbol{K}_{g} \boldsymbol{J}_{g}(\boldsymbol{q}) \dot{\boldsymbol{q}} \leq \mathbf{0} \end{aligned} \tag{6}$$

对角矩阵$K_f \in \mathbb{R}^{F\times F}, K_{g}\in\mathbb{R}^{G\times G}$均为正项。矩阵$K_f$和$K_g$决定了约束$\dot f$和$\dot g$的最大速度与约束值的比值。

不等式约束的可行性约束如图2所示。当$g(q) < 0$时，约束速度的上界为$\dot g_{max} > 0$，表明仍有可能接近约束边界。然而，当$g(q) > 0$时，约束速度$\dot g_{max}$的上界应小于零。

与式(2)和式(3)的推导类似，我们有：

$$c(\boldsymbol{q},\dot{\boldsymbol{q}},\boldsymbol{\mu})=\begin{bmatrix}\boldsymbol{f}(\boldsymbol{q})+\boldsymbol{K}_f\boldsymbol{J}_f(\boldsymbol{q})\dot{\boldsymbol{q}}\\\boldsymbol{g}(\boldsymbol{q})+\boldsymbol{K}_g\boldsymbol{J}_g(\boldsymbol{q})\dot{\boldsymbol{q}}+\frac12\boldsymbol{\mu}^2\end{bmatrix}=\mathbf{0} \tag{7}$$

$$\dot{\boldsymbol{c}}(\boldsymbol{q},\dot{\boldsymbol{q}},\ddot{\boldsymbol{q}},\boldsymbol{\mu},\dot{\boldsymbol{\mu}})=\underbrace{\begin{bmatrix}\boldsymbol{K}_f\boldsymbol{J}_f(\boldsymbol{q})&\boldsymbol{0}\\\boldsymbol{K}_g\boldsymbol{J}_g(\boldsymbol{q})&\mathrm{diag}(\boldsymbol{\mu})\end{bmatrix}}_{\boldsymbol{J}_c(\boldsymbol{q},\boldsymbol{\mu})}\begin{bmatrix}\ddot{\boldsymbol{q}}\\\dot{\boldsymbol{\mu}}\end{bmatrix}+\underbrace{\begin{bmatrix}\boldsymbol{J}_f(\boldsymbol{q})\dot{\boldsymbol{q}}+\boldsymbol{K}_f\boldsymbol{b}_f(\boldsymbol{q},\dot{\boldsymbol{q}})\\\boldsymbol{J}_g(\boldsymbol{q})\dot{\boldsymbol{q}}+\boldsymbol{K}_g\boldsymbol{b}_g(\boldsymbol{q},\dot{\boldsymbol{q}})\end{bmatrix}}_{\psi(\boldsymbol{q},\dot{\boldsymbol{q}})}=\boldsymbol{0} \tag{8}$$

式中$\boldsymbol{b}_f(\boldsymbol{q},\dot{\boldsymbol{q}})=\dot{\boldsymbol{q}}^\mathsf{T}\boldsymbol{H}_f(\boldsymbol{q})\dot{\boldsymbol{q}}$, $\boldsymbol{b}_g(\boldsymbol{q},\dot{\boldsymbol{q}})=\dot{\boldsymbol{q}}^\mathsf{T}\boldsymbol{H}_g(\boldsymbol{q})\dot{\boldsymbol{q}}$, $\boldsymbol{H}_f\in\mathbb{R}^{F\times Q\times Q},\boldsymbol{H}_g(\boldsymbol{q})\in\mathbb{R}^{G\times Q\times Q}$分别为$f(q)、g(q)$的Hessians矩阵。我们可以构造关节加速度为:

$$\begin{bmatrix}\ddot{\boldsymbol{q}}\\\dot{\boldsymbol{\mu}}\end{bmatrix}=-\boldsymbol{J}_c^\dagger(\boldsymbol{q},\boldsymbol{\mu})\boldsymbol{\psi}(\boldsymbol{q},\dot{\boldsymbol{q}})+\boldsymbol{N}_c(\boldsymbol{q},\boldsymbol{\mu})\boldsymbol{\alpha} \tag{9}$$

分别用雅可比矩阵$J_c(\boldsymbol{q},\boldsymbol{\mu})$的伪逆$J_{c}^{\dagger}(\boldsymbol{q},\boldsymbol{\mu})$和零空间矩阵$\boldsymbol{N}_c(\boldsymbol{q},\boldsymbol{\mu})$。方程(9)中的第一项是维持约束流形(7)曲率的必要加速度，第二项是约束的切空间加速度。

当从点$[\boldsymbol{q}(0),\dot{\boldsymbol{q}}(0),\boldsymbol{\mu}(0)]\in\{(\boldsymbol{q},\dot{\boldsymbol{q}},\boldsymbol{\mu})|\boldsymbol{c}(\boldsymbol{q},\dot{\boldsymbol{q}},\boldsymbol{\mu})=\boldsymbol{0}\}$开始，在$\alpha$上采样时，关节加速度$\ddot{q}$和相应的动作$a$满足约束条件。

Viability Acceleration Bound

在机器人和其他机械系统中，考虑执行器的速度约束是很重要的。此外，加速度应该适当地有界，以避免超调。我们再次使用可行性的概念来确定加速度的上界和下界:

$$\boldsymbol{a}_{u}=\max\left(\min\left(\boldsymbol{a}_{\max},-\boldsymbol{K}_{a}(\boldsymbol{q}-\boldsymbol{v}_{\max})\right),\boldsymbol{a}_{\min}\right)$$

$$\boldsymbol{a}_{l}=\min\left(\max\left(\boldsymbol{a}_{\min},-\boldsymbol{K}_{a}\left(\boldsymbol{q}-\boldsymbol{v}_{\min}\right)\right),\boldsymbol{a}_{\max}\right)$$

以最小和最大关节速度极限$v_{min,max}$和加速度极限$a_{min,max}$，$K_a > 0$为常数。可行加速度区域如图3所示。与可行性约束类似，加速度的可行区域根据关节速度的状态进行修改。这种技术有效地防止了超调。

Error Correction and Control Action Selection

对于时间连续系统，以一定的采样率获得状态，并应用周期一定的动作。这种时间离散化导致每个时间步上的约束违反。因此，我们增加了一个误差校正项。我们构造了一个具有对角矩阵$K_c$的P-controller。

$$\begin{bmatrix}\ddot{\boldsymbol{q}}_E\\\dot{\boldsymbol{\mu}}_E\end{bmatrix}=-\boldsymbol{J}_c^\dagger\boldsymbol{K}_c\boldsymbol{c}(\boldsymbol{q},\dot{\boldsymbol{q}},\boldsymbol{\mu}) \tag{10}$$

将式(9)与式(10)结合，得到作用于系统的关节加速度：

$$\begin{bmatrix}\ddot{\boldsymbol{q}}\\\dot{\boldsymbol{\mu}}\end{bmatrix}=-\boldsymbol{J}_c^\dagger(\boldsymbol{q},\boldsymbol{\mu})\left[\boldsymbol{K}_c\boldsymbol{c}(\boldsymbol{q},\dot{\boldsymbol{q}},\boldsymbol{\mu})+\boldsymbol{\psi}(\boldsymbol{q},\dot{\boldsymbol{q}})\right]+\boldsymbol{N}_c(\boldsymbol{q},\boldsymbol{\mu})\boldsymbol{\alpha} \tag{11}$$

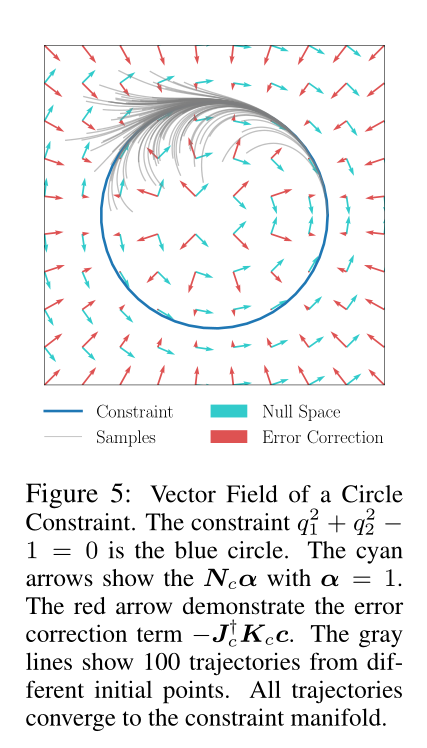
RHS上的第一项是维持约束条件所需的加速度/速度RHS上的第二项是可以自由探索的正切加速度。图5给出了圆约束的误差校正项和零空间项的向量场。灰色曲线表示采样轨迹由于误差修正而收敛到约束流形。

控制作用可由不同级别的$\boldsymbol{a}=\boldsymbol{\Lambda}(\ddot{\boldsymbol{q}})$确定。例如，我们可以使用逆动力学模型来计算通过扭矩命令控制机器人时的关节扭矩。我们也可以应用积分方法来确定期望的位置/速度，然后使用足够精确的跟踪控制器(例如PID控制器+前馈项)来跟踪期望的轨迹。

Null Space Convention

正交零空间矩阵$N_c$可以通过SVD或QR分解来确定。然而，零空间基的表示并不是唯一的。采用数值分解方法计算的零空间基很难保持一致性。为了解决这个问题，文章提出了一个保证零空间基唯一性的约定。

零空间矩阵$N_c$的每一列是一个单位向量，表示方向为$[\ddot q \ \dot u]$。然而，这个单位矢量有时可能主要贡献于松弛变量的部分，关节加速度的项可能非常小。因此，由$\alpha \in [\alpha_{min}, \alpha_{max}]$得到的关节加速度只能覆盖加速度的一小部分。如图4所示，红色箭头为切空间的单位基向量，通过通用比例因子得到的可达关节加速度只能覆盖部分可行关节加速度，如图4所示红色区域。为了缓解前面提到的问题，我们计算零空间矩阵$N_{c}^{R}=RCEF(N_c)$的简化列梯形（Reduced Column Echlon Form, RCEF）。给定矩阵的 RCEF 是唯一的，我们得到零空间的唯一基。此外，对于RCEF，包含前导1的每行在其所有其他条目中都有零。一般来说，存在N个独立的关节，它们的加速度可以由$\alpha$单独决定，其中N是零空间的维数。

也可以定义$\alpha$的可行范围为$\alpha \in [\ddot q_{i, min}, \ddot q_{i, min}]$。通过这种约定，关节加速度能够覆盖整个可行范围。零空间基和可行域如图4中蓝色向量和蓝色区域所示。

ATACOM算法流程：

原文：RL in Constraint Manifold.pdf

引用：Liu P, Tateo D, Ammar H B, et al. Robot reinforcement learning on the constraint manifold[C]//Conference on Robot Learning. PMLR, 2022: 1357-1366.